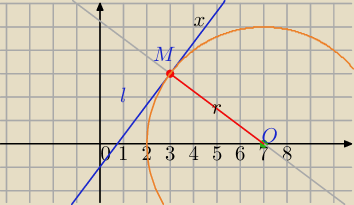
/ akcjadesperacja: Przez punkt P, znajdujący się w odległości 5 pierw17 od środka O(7, 0) okręgu, poprowadzono dwie proste l i k, styczne do danego okręgu odpowiednio w punktach M i N (zobacz rysunek obok). Wiedząc, że prosta l ma równanie 4x – 3y – 3 = 0, oblicz pole czworokąta MONP. https://www.fotosik.pl/zdjecie/603145b6cd9f3ca1

Mila:

	4
l: 4x – 3y – 3 = 0,⇔y=		x−1
	3

1) Styczna jest prostopadła do promienia w punkcie styczności. O(7,0) p⊥l i O∊p

	3		3		21
p: y=−		x+b i −		*7+b=0⇔b=
	4		4		4

	3		21
p: y=−		x+
	4		4

2) wsp. punktu M:

4		3		21
	x−1=−		x+		⇔
3		4		4

x=3 i y=3 M=(3,3) r=|OM|=5 |OP|=5√17 przeciwprostokątna w ΔOMN |MP|²+r²=|OP|² x²=25*17−25 x²=25*16 x=5*4=20 , |MP|=20 3)

	1		1
PΔOMP=		*|OM|*|MP|=		*5*20=50
	2		2

4) Prosta OP jest osią symetrii czworokąta MONP. P_MONP=2*5=100 ==========

Satan: https://matematykaszkolna.pl/forum/372562.html Oczywiście "Pan" miał już rozwiązanie, ale ciężko spróbować samemu według instrukcji