optymalizacja josia88: Rozpatrujemy wszystkie ostrosłupy prawidłowe trójkątne, w których suma długości wszystkich krawędzi jest równa 30. Podaj wzór funkcji wyrażającej objętość takiego ostrosłupa w zależności od długości jego krawędzi podstawy. Określ jej dziedzinę. Wyznacz wymiary tego z ostrosłupów, który ma największą objętość. Oblicz tę objętość. Liczę na pomoc, zatrzymałam się na pochodnej funkcji ale wyszła mi bardzo brzydka i nie wiem czy coś źle zrobiłam czy po porostu muszę sobie poradzić z czymś takim

Jerzy: Nie wszystkie pochodne są ładne.

Jerzy: Taką masz funkcję : https://matematykaszkolna.pl/forum/369127.html ?

josia88: H mi wyszło takie: √^4a2₅ −20a +100

josia88: reszta tak samo

josia88: oki znalazłam swój błąd. nie rozumiem tego ostatniego kroku co zrobiła Basia. Czemu nagle 3a²√2 zmienia się na a²√2

josia88: i przede wszystkim: jak zrobić z takiego wyrażenia pochodna

Jerzy: Pochodną się oblicza, nie "robi".

Kristof: dobrze przepraszam: jak obliczyć z takiego wyrażenia pochodna? nie pomijając mojego wcześniejszego zapytania

Jerzy: Co do pochodnej ... włacz a² pod pierwiastek.

Jerzy: Przecież skrociła licznik i mianownik przez 3.

josia88:

√3
	√23a6− 20a5 + 100a4 taka mi wyszła funcja. pomoże mi ktoś obliczyć
12

pochodną z tego? powstaje funkcja f(x)= ²₃a⁶− 20a⁵ + 100a⁴ ale dalej mi wychodzą złe wyniki.. help

josia88: chciałam napisać że rozważamy funcję f(x)= ²₃a⁶− 20a⁵ + 100a⁴ . Bardziej formalnie− specjalnie dla Ciebie. Później mi źle wychodzi.

Jerzy: 16:56 napisałaś inna funkcję.

Jerzy: Przecież o 16:56 masz wielomian pod pierwiastkiem, a o 17:02 już pierwiastka nie ma.

Jerzy:

	2
Co to znaczy : "powstaje funkcja f(x) =		a6 − 20a5 + 100a4" ?
	3

Z czego powstaje ta funkcja ?

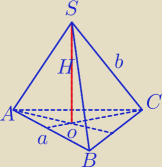
Mila: 1) 3a+3b=30⇔a+b=10

	2		a√3		a√3
|OC|=		*		=
	3		2		3

2) W ΔSOC: H²+|OC|²=b²

	a√3
H2+(		)2=(10−a)2 i a∊(0,10)
	3

	1
H2=100−20a+a2−		a2
	3

	2		2
H2=		a2−20a+100⇔H2=		*(a2−30a+150)
	3		3

Z. a²−30a+150>0 i a∊(0,10)⇔ a∊(0, 15−5√3) 15−5√3≈6,4 sprawdź! 3)

	√2
H=		*√a2−30a+150
	√3

4)

	1		a2√3		√2
V(a)=		*		*		*√a2−30a+150⇔
	3		4		√3

	√2
V(a)=		*√a2−30a+150
	12

	√2
V(a)=		*√a6−30a5+150a4
	12

	√2		6a5−150a4+600a3
V'(a)=		*
	12		2√a6−30a5+150a4

V'(a)=0 i a∊D 6a⁵−150a⁴+600a³=0 a³*(6a²−150a+600)=0 a²−25a+100=0⇔a=5 lub a=20∉D V'(a)>0⇔a<5 lub a>20⇔ dla a=5 funkcja V(a) ma maksimum lokalne

	125√2
V(5)=
	12

================== Czyli to jest czworościan foremny!

Mila: O! ja pisałam, a tu była awantura, nieładnie

josia88: Przykro mi Mila, przepraszam, ale bardzo dziękuję za pełen profesjonalizm

josia88: ojej czemu moje wiadomości zostały usunięte? nie podoba się komuś że pisałam prawde? niestety trochę przykre. Ale mimo tego pozdrawiam Pana Jerzego, życzę powodzenia w życiu.

Jerzy: Ja Cię też pozdrawiam

josia88: mam pytanko jeszcze do Mili nie rozumiem trochę jakim sposobem obliczyłaś tę pochodną i czy mój sposób na rozważnie funkcji f(x) jest poprawny? w tym przypadku wychodzi f(x)= a⁶ −30a⁵+150a⁴. wyciągam a⁴ ale wychodzi brzydka delta

Jerzy: Sama widzisz,że nie potrafisz liczyć pochodnych, co już Ci napisałem.

Jerzy: I co Cię obchodzi funkaja: f(x) = a⁶ − 30a⁵ + 150a⁴ ? Szukasz miejsc zerowych funkcji: 6a⁵ −150a⁴ + 600a²

Jerzy: ....... + 600a³

josia88: jejku przepraszam że tego nie rozumiem Jerzy nie musisz się denerwować. nie chcę robić niepotrzebnej dramy dlatego zwróciłam się z pytaniem do Mili.

Jerzy: Uważaj:

	1		f'(x)
(		)' =		.
	√f(x)		2√f(x)

Teraz pochodna sie zeruje, gdy : f'(x) = 0

Jerzy: I popatrz co zrobiła Mila .... 6a⁵ − 150a⁴ + 600a³ = 0

Mila: V(a)=√a⁶−30a⁵+150a⁴ ( pomijam stałą przed pierwiastkiem)

	1
V'(a)=		* (a6−30a5+150a4)'
	2√a6−30a5+150a4

	6a5−150a4+600a3
=
	2√a6−30a5+150a3

V(a) posiada ekstremum jeżeli V'(a)=0 i pochodna zmienia znak przy przejściu przez miejsca zerowe Czyli licznik pochodnej przyrównujesz do zera, bo mianownik musi byc różny od zera. i dalej masz tak zrobione. Poćwicz pochodną z g(x)=√x

	1		2x		x
(√x2+1)'=		*(x2+1)'=		=
	2√x2+1		2√x2+1		√x2+1

josia88: czy to co napisałeś w przedostatnim wpisie jest konieczne skoro i tak liczymy pochodną z tej funkcji f(x) przepraszam że może wydawać ci się to głupie pytanie ale jak zauważyłeś pochodna nie jest moją mocną stroną, dlatego właśnie tutaj jestem.

Jerzy: Popatrz wyżej, ta pochodna się zeruje wtedy, gdy licznik przyjmuje wartość zero.

josia88: dziękuje za pomoc. w szkole nie omawialiśmy pochodnej z √x stad wynika moja niewiedza.

Jerzy: Ćwicz pochodne, bez tego nie dasz rady dalej....

josia88: trudno było coś ćwiczyć jeśli się nie wiedziało że coś takiego wgl istnieje. teraz już wiem i będę ćwiczyć

Jerzy: A jak będziesz miała problem .... wrzucaj, a my pomożemy.

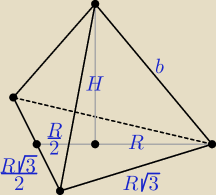
Bogdan: Wtrącę swoje trzy grosze Możemy przyjąć dowolną zmienną, tu dla wygody obliczeń przyjąłem R − długość promienia okręgu opisane na podstawie ostrosłupa prawidłowego trójkątnego. b + R√3 = 10 ⇒ b = 10 − R√3 ⇒ b² = 100 − 20R√3 + 3R² H² = b² − R² ⇒ H = √ 100 − 20R√3 + 2R² Objętość ostrosłupa

	1		3		√6
V =		*		R2√3*√ 100−20R√3+2R2 =		*√ R6 − 10√3R5 + 50R4
	3		4		4

	√6
V(R) =		* √ f(R) , f(R) = R6 − 10√3R5 + 50R4
	4

Wyznaczamy maksimum funkcji f(R):

	25		100
f'(R) = 6R5 − 50√3R4 + 200R3 = 6R3(R2 −		R +		) =
	√3		3

	5		20		5
= 6R3(R −		)(R −		), maksimum dla R =
	√3		√3		√3

Długość krawędzi podstawy R√3 = 5, długość krawędzi bocznej b = 10 − 5 = 5, ostrosłup jest czworościanem foremnym o krawędzi długości 5.