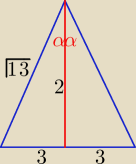
cosinus kąta rozwarcia stożka asiak98: Oblicz cosinus kąta α rozwarcia stożka o objętości 6π, którego długość wysokości równa się 2. No więc z objętości 6π=2/3π*r² wyliczyłem, że r jest równe 3 Z tw. pitagorasa wyliczyłem tworzącą równą √13 Jak mogę dalej wyliczyć cosinus kąta α mając te dane?

Eta: cos(2α)= −5/13

Eta: cos(2α)= 1−2sin²α sinα= 3/√13 .......... dokończ

asiak98: Ale to kątem rozwarcia strożka nie jest własnie cos 2α z rysunku?

Eta: https://matematykaszkolna.pl/strona/1003.html to może tu się podszkolisz !

asiak98: Chyba załapałem. I prześledziłem Twoje obliczenia. Pierw z twierdzenia cosinusów cos(2α)= −5/13 −5/13 = 1 − 2sin² α −18/13 = −2 sin² α sin α = 3√2/√2√13 i po skróceniu zostaje 3/√13 Potem użyłem jedynki trygonometrycznej 1 = 9/13 + cos² α cos² α = 4/13 cos α = 2/√13 Jest ok?

Eta: Nie masz podać cos(2α) a nie cos α cos(2α)= 1−sin²α=................... dokończ i nie kombinuj ...

Eta: I co? dokończyłeś?