Wyznacz dziedzinę i miejsce zerowe funkcji
Uczę się do maturki: Wyznacz dziedzinę i miejsce zerowe funkcji g(x)=log2(x3+x2−2x)
19 mar 19:05
Dziedzina: x3+x2−2x>0
x(x2+x−2)>0
x(x+2)(x−1)>0
19 mar 19:15
Uczę się do maturki: Czyli miejsca zerowe to −2 i 1 ?
19 mar 19:20
Eta:
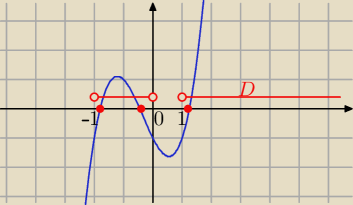
g(x)=0 ⇔ log
2(x
3+x
2−2x)=0 ⇔ x
3+x
2−2x= 2
0=1
x
3+x
2−2x−1=0 i x∊( −2,0)u (1,
∞)
Dokładnych miejsc Ci nie podam
ale jak widać są trzy miejsca zerowe ∊ D
19 mar 19:32
Eta:
Sprawdź czy dobrze przepisałaś tę funkcję ?
19 mar 19:33
Uczę się do maturki: Sory powinno być g(x)=log2(2x3+x2−2x)
19 mar 19:36
Eta:
No właśnie ..

19 mar 19:41
Eta:
Na podstawie tego co podałam spróbuj rozwiązać samodzielnie
podaj wynik , to sprawdzę
19 mar 19:42
Uczę się do maturki: log
2(2x
3+x
2−2x)=0
2x
3+x
2−2x=2
0=1
2x
3+x
2−2x−1=0
I teraz co dalej jak namalować wykres ?

19 mar 19:50
Eta:
Nic nie "malować"
x2(2x+1)−(2x+1)=0
(2x+1)(x2−1)=0
x= ... v x=... v x=...
i sprawdź koniecznie czy należą do dziedziny
19 mar 19:52
Eta:
Dziedzinę musisz na nowo wyznaczyć ! bo tamta jest do innej funkcji
19 mar 19:56
Uczę się do maturki: Ja chce się tylko nauczyć ja nic nie wiem, nie byłem na tych lekcjach

19 mar 20:03
Eta:

19 mar 20:07
Uczę się do maturki: 2x+1=0
2x=−1 /:2
x=−1/2
x2−1=0
x2=1
x=1
coś takiego ?
19 mar 20:15
Eta:
x2−1=0 −−− ma dwa rozwiązania
(x−1)(x+1)=0
.........
19 mar 20:16
Uczę się do maturki: i jeszcze x=−1
19 mar 20:17
Eta: Tak
19 mar 20:18
Uczę się do maturki: Teraz dziedzinę
2x3+x2−2x>0
x(2x2+x−2)>0
19 mar 20:19
Uczę się do maturki: i co dalej ?
19 mar 20:19
Eta:
Dziedzina ustalona?
2x
3+x
2−2x>0
x(2x
2+x−2)>0 i licz "deltuszkę"

19 mar 20:30
Uczę się do maturki: Δ=1−4*2*(−2)=1+16=17
19 mar 20:38
Uczę się do maturki: I co dalej ?
19 mar 20:38
Eta:
miejsca zerowe .........
19 mar 20:39
19 mar 20:41
Eta:
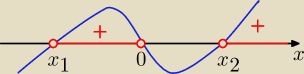
D: x∊ (.....................
19 mar 20:41
Eta:
No i piknie

teraz dokończ .....
19 mar 20:42
Uczę się do maturki: Mogę dowiedzieć się jak powstał ten wykres ?
19 mar 20:43
Eta:
x( x−x1)(x−x2)>0
"wężyk" od prawej z góry przez miejsca zerowe ...
19 mar 20:48
19 mar 20:48
Uczę się do maturki: Dzięki
19 mar 21:10
Eta: Na zdrowie łap.......


19 mar 21:11
 g(x)=0 ⇔ log2(x3+x2−2x)=0 ⇔ x3+x2−2x= 20=1
x3+x2−2x−1=0 i x∊( −2,0)u (1,∞)
Dokładnych miejsc Ci nie podam
ale jak widać są trzy miejsca zerowe ∊ D
g(x)=0 ⇔ log2(x3+x2−2x)=0 ⇔ x3+x2−2x= 20=1
x3+x2−2x−1=0 i x∊( −2,0)u (1,∞)
Dokładnych miejsc Ci nie podam
ale jak widać są trzy miejsca zerowe ∊ D





 D: x∊ (.....................
D: x∊ (.....................
 teraz dokończ .....
teraz dokończ .....

