Wyznacz wszystkie liczby rzeczywiste x spełniające równanie 2sin^2x-cos2x=1 Pomocy!: Męczę się z tym zadaniem już kilka dni, nie potrafię zrozumieć rozwiązania. Oto jego treść: Wyznacz wszystkie liczby rzeczywiste x spełniające równanie 2sin²x−cos2x=1. Oblicz sumę wszystkich rozwiązań tego równania należących do przedziału <0,32π>.

	√2
Pierwszą część zrobiłem, na początku pozbywając się cosinusa, wtedy sinus wychodził ±
	2

	π		π
a wtedy x=		+kπ lub x=−		+kπ.
	4		4

Za drugim podejściem pozbyłem się na początku sinusa i

	π		kπ
zostało mi piękne cos2x=0, a wtedy x=		+		. Dwa różne wyniki, nie wiem, czy tak
	4		2

powinno być, ale już uznałem, że ta druga metoda (z zostawieniem cosinusa) jest lepsza. No to ok, mam

	π		kπ
x=		+		i podstawiam sobie za k 0, 1, 2, 3, ... i zauważam, że to ciąg arytmetyczny
	4		2

o

	π
różnicy równej		. Granicą przedziału jest 32π. Za k podstawiam 62 a wtedy:
	2

	π		62π		125π
x=		+		=		=31,25π jeszcze trochę do granicy zostało, więc idę dalej
	4		2		4

Dla k=63 mam x=31,75π Dla k=64 mam x=32,25π I jestem w kropce. Zrobiłem tak jak Eta https://matematykaszkolna.pl/forum/366335.html

	129π
za n podstawiając 64 (a wtedy an=		i suma wyszła 1040π, jeśli nie pomyliłem się w
	4

rachunkach). Natomiast tutaj−> https://www.matematyka.pl/428387.htm ta suma wychodzi 992π, ale tamtego rozwiązania w ogóle nie rozumiem. Proszę o pomoc, naprawdę chciałbym zrozumieć trygonometrię

aniabb: to nie są różne wyniki −π/4 +π/2 = −π/4 +2π/4 = π/4 czyli zamiast 2 z krokiem kπ masz jedno co kπ/2 dla k=64 jesteś poza granicą ostatni to dla k=63 x=31.75π więc 127π/4 ale wyrazów w ciągu masz 64 bo zacząłeś od 0

aniabb: a na matematyka.pl autor nie uwzględnił, że zaczyna od 0 i zamiast mnożyć przez 31 powinien przez 32 i dlatego ma zaniżony wynik

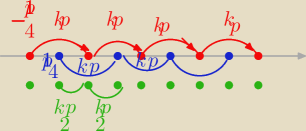
aniabb: to zamazane to 1/4 bo tu nie ma opcji kasowania jak coś było dawno wcześniej narysowane a ma to tylko obrazować zmianę kroku z kπ na kπ/2

Pomocy!: Dziękuję za zobrazowanie tego przejścia, narysowałem sobie dokładny wykres sinusa i teraz

	π		kπ
widzę, że wszystko wychodzi dobrze i x=		+		, niepotrzebnie przyjąłem samo kπ, bo
	4		2

	5π		3π
wtedy punkt jest po π (		), a zależało mi na punkcie		.
	4		4

I no tak, zapomniałem o pierwszym wyrazie z k=0. Nie wiedziałem też, które k wybrać przy ostatnim wyrazie. Wybrałem k=64, bo uznałem, że dla k=63 x=31,75π jeszcze do tej granicy trochę zostało, ale faktycznie nie powinienem przekraczać 32π. Czyli mam:

	π		kπ
x=		+		i k∊ℤ
	4		2

	π		π		π		π		127π
a1=		przy k=0, r=		, an=		+63*		=		, n=64
	4		2		4		2		4

	a1+an		π   127π   + 4   4
S=		*n=		*64 = 1024π
	2		2

Czy to jest dobrze?

annabb: Tak

Pomocy!: Bardzo dziękuję za pomoc