Dwusieczna i przystawanie trojkatow
Krzysiek60:
Zadanie
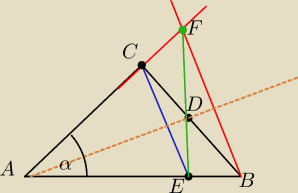
Dwusieczna kata A w trokacie ABC przecina bok BC w punkcie D
Z wierzcholka B i C poprowadzono proste prostopadle do AD przecinajace proste AC i AB
odpowiednio w puntach E i F
Wykaz ze ΔABC ≡ΔAEF oraz ze punkty EDF sa wspoliniowe
Jedynie co wiem
CEIIFB to z warunku zadania (dwie proste prostopadle do trzeciej prostej sa do siebie
rownolegle
Kat CAE jest wspolnym katem dla tych trojkatow jesliby udalo mi sie wykazac ze EB=CF to
czwrorokat EBFC bedzie trapezem rownoramiennym
ii wtedy te punkty beda wspoliniowe bo beda lezezec na jego przekatnej
Chyba znalazlem rozwiazanie bo ostanio robilem zadanie z dwusieczna kata
Skoro punkt D lezy na dusiecznej kata CAE to trojkat CFD≡EDB
Z przystawania tego wynika ze CD= DE ED= BB oraz co mnie cieszy CF= EB
ΔABC≡AEF cecha BKB
∡CAB wsolny
EF=BC
AB= AF
Prosze o sprawdzenie
8 mar 20:03
8 mar 20:57
Krzysiek60: Dziekuje
8 mar 21:00
Krzysiek60: Jesli mozesz to tez takie zadanie bo sobie przypominam ze bylo
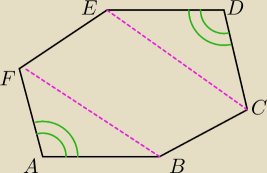
Wypukly szesciokat ABCDEF ma wszystkie boki rownej dlugosci i kat BAF= katowi CDE Wykaz ze CEII
BF
(bylo w tym samy czasie bo to z jednego zbioru . dziekuje
8 mar 21:04
wolf: Masz do szkoły na jutro?
8 mar 21:06
Krzysiek60: Oczywiscie ?

)
8 mar 21:08
wolf: ok
8 mar 21:16
iteRacj@:
do szkoły trzeba mieć odrobione lekcje
założenie |AB|=|CD|=|EF|=|BC|=|DE|=|FA|
|<BAF|=|<CDE|
teza CEIIBF
|DE|=|FA|,|AB|=|CD|
|<BAF|=|<CDE|
ΔBAF ≡ ΔCDE (bkb) ⇒ |CE|=|BF|
ponieważ |EF|=|BC| i |CE|=|BF| ⇒ czworokąt EFBC jest równoległobokiem
więc CE∥BF i CB∥EF
8 mar 22:07
Krzysiek60: Dobry wieczor i dziekuje Ci

Wszystko poszlo sie ......... i faktycznie czesc zadan sie powtarza (robilem je wczesniej
NIe powinno ich byc juz duzo ktore sie powtorze no ale jesli to bede mial inny sposob .
8 mar 22:17
iteRacj@:
a spróbuj poszukać przez Google, wpisując swój nick i zadanie, łatwiej tak coś znaleźć niż
przez tutejszą wyszukiwarkę (może w Kalifornii lepiej indeksują?)
8 mar 22:38
Krzysiek60: Wiesz tak patrze i moze jeszcze ze dwa zadania wstawilem wczesniej
Wiec wstawie je jeszcze raz . Krzywdy nie bedzie

8 mar 22:41
 Zadanie
Dwusieczna kata A w trokacie ABC przecina bok BC w punkcie D
Z wierzcholka B i C poprowadzono proste prostopadle do AD przecinajace proste AC i AB
odpowiednio w puntach E i F
Wykaz ze ΔABC ≡ΔAEF oraz ze punkty EDF sa wspoliniowe
Jedynie co wiem
CEIIFB to z warunku zadania (dwie proste prostopadle do trzeciej prostej sa do siebie
rownolegle
Kat CAE jest wspolnym katem dla tych trojkatow jesliby udalo mi sie wykazac ze EB=CF to
czwrorokat EBFC bedzie trapezem rownoramiennym
ii wtedy te punkty beda wspoliniowe bo beda lezezec na jego przekatnej
Chyba znalazlem rozwiazanie bo ostanio robilem zadanie z dwusieczna kata
Skoro punkt D lezy na dusiecznej kata CAE to trojkat CFD≡EDB
Z przystawania tego wynika ze CD= DE ED= BB oraz co mnie cieszy CF= EB
ΔABC≡AEF cecha BKB
∡CAB wsolny
EF=BC
AB= AF
Prosze o sprawdzenie
Zadanie
Dwusieczna kata A w trokacie ABC przecina bok BC w punkcie D
Z wierzcholka B i C poprowadzono proste prostopadle do AD przecinajace proste AC i AB
odpowiednio w puntach E i F
Wykaz ze ΔABC ≡ΔAEF oraz ze punkty EDF sa wspoliniowe
Jedynie co wiem
CEIIFB to z warunku zadania (dwie proste prostopadle do trzeciej prostej sa do siebie
rownolegle
Kat CAE jest wspolnym katem dla tych trojkatow jesliby udalo mi sie wykazac ze EB=CF to
czwrorokat EBFC bedzie trapezem rownoramiennym
ii wtedy te punkty beda wspoliniowe bo beda lezezec na jego przekatnej
Chyba znalazlem rozwiazanie bo ostanio robilem zadanie z dwusieczna kata
Skoro punkt D lezy na dusiecznej kata CAE to trojkat CFD≡EDB
Z przystawania tego wynika ze CD= DE ED= BB oraz co mnie cieszy CF= EB
ΔABC≡AEF cecha BKB
∡CAB wsolny
EF=BC
AB= AF
Prosze o sprawdzenie
 )
)
 do szkoły trzeba mieć odrobione lekcje
założenie |AB|=|CD|=|EF|=|BC|=|DE|=|FA|
|<BAF|=|<CDE|
teza CEIIBF
|DE|=|FA|,|AB|=|CD|
|<BAF|=|<CDE|
ΔBAF ≡ ΔCDE (bkb) ⇒ |CE|=|BF|
ponieważ |EF|=|BC| i |CE|=|BF| ⇒ czworokąt EFBC jest równoległobokiem
więc CE∥BF i CB∥EF
do szkoły trzeba mieć odrobione lekcje
założenie |AB|=|CD|=|EF|=|BC|=|DE|=|FA|
|<BAF|=|<CDE|
teza CEIIBF
|DE|=|FA|,|AB|=|CD|
|<BAF|=|<CDE|
ΔBAF ≡ ΔCDE (bkb) ⇒ |CE|=|BF|
ponieważ |EF|=|BC| i |CE|=|BF| ⇒ czworokąt EFBC jest równoległobokiem
więc CE∥BF i CB∥EF
 Wszystko poszlo sie ......... i faktycznie czesc zadan sie powtarza (robilem je wczesniej
NIe powinno ich byc juz duzo ktore sie powtorze no ale jesli to bede mial inny sposob .
Wszystko poszlo sie ......... i faktycznie czesc zadan sie powtarza (robilem je wczesniej
NIe powinno ich byc juz duzo ktore sie powtorze no ale jesli to bede mial inny sposob .
