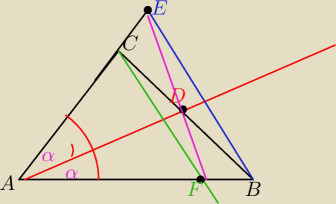
Przystawanie tojkatow 5-latek: Dwusieczna kata A w trojkacie ABC przecina bok BC w punkcie D Z wierzcholka B i C poprowadzono proste prostopadle do AD przecinajace proste AC i AB odpowiednio w punktach E i F Wykaz ze ΔABC ≡ΔAEF oraz z epunkty EDF sa wspoliniowe Rysunek dokladny do zadania mam zrobiony w zeszycie Tutaj prawie mi sie udalo jest wskazowka do zadania zeby wykazac ze czworokta BECF jest trapezem rownoramiennym Otoz odcinki Be i CF sa rownolegle bo sa prostopadle do prostej AD Teraz mam pytanie Czy dwusieczna AD jest osia symetrii tego czorokata ? ================================================= Jesli tak to os symetrii ma trapez rownoramienny wiec punktD jest punktem symetrii tego trapezu W zwiazku z tym ΔCDE≡BDFB na podstawie cechy BKB CD=DB ED=DF Kąt EDC= katowi BDF jako wierzcholkowe Wobec tych rownosci CE=FB Wiec mamy trapez rownoramenny W trapezie rownoramiennym przekatne sa rowne to EF= BC Zastanawiam sie nad cecha przystawania trojkato ABC≡AEF

5-latek:

5-latek: jesli mozesz to najpierw powiedz czy do tego momentu mam wszystko dobrze i potem z tym przystawaniem

Mila: Dwusieczna AD jest zawarta w osi symetrii tego trapezu. Punkt D ∊osi symetrii tego trapezu . ( trapez nie ma środka symetrii)

5-latek: Dobrze . dzieki Teraz mysle nad przystawaniem tych trojkatow ΔABC≡ΔAEF Cecha BKB i AB=AE i ∡EAB wspolny

Mila: albo bbb AB≡AE AC≡AF EF≡BC

5-latek: Dziekuje Ci i dobranoc

Mila: Dobranoc