Dany jest Δ równoramienny ABC w którym AC= BC =2 i ∡ABC=75. Zatem oblicz długość
alinka: Dany jest Δ równoramienny ABC w którym AC= BC =2 i ∡ABC=75. Zatem oblicz długość AB i środkowej
AE
1 mar 10:38
Krzysiek60:
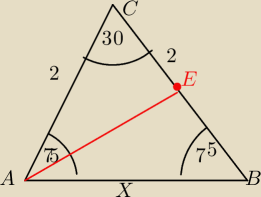
Z twierdzenia cosinusow oblicz dlugosc AB
Dlugosc srodkowej AE
|AE|= 0,5
√2(AC2+AB2)−BC2
1 mar 10:55
aniabb:
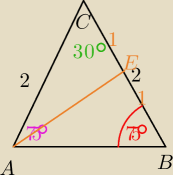
tw. cosinusów
AB
2=4+4+4
√3
AE
2=4+1+
√3
1 mar 10:55
Krzysiek60: Dzien dobry

Zaraz bede zmykal
1 mar 10:59
alinka: a bez użycia twierdzenia cosinusów?
1 mar 11:11
aniabb: zrób sobie trójkąt prostokątny prowadząc wysokość z A i dwa razy twierdzenie pitagorasa na
każdy szukany odcinek
1 mar 11:18
1 mar 11:23
aniabb: dla środkowej podobnie tylko potem pitagoras w górę
AE2= 12 +(√3−1)2
1 mar 11:25
alinka: ♥♥
1 mar 13:02
Krzysiek60: A w czym przeszkadza tw cosinusow ?
1 mar 13:52
 Z twierdzenia cosinusow oblicz dlugosc AB
Dlugosc srodkowej AE
|AE|= 0,5√2(AC2+AB2)−BC2
Z twierdzenia cosinusow oblicz dlugosc AB
Dlugosc srodkowej AE
|AE|= 0,5√2(AC2+AB2)−BC2
 tw. cosinusów
AB2=4+4+4√3
AE2=4+1+√3
tw. cosinusów
AB2=4+4+4√3
AE2=4+1+√3
 Zaraz bede zmykal
Zaraz bede zmykal
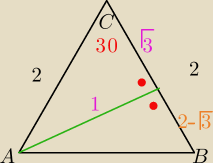 a nie tyle pitagoras co związki w trójkącie 30 60 90 https://matematykaszkolna.pl/strona/2280.html
a potem AB2=12+(2−√3)2
a nie tyle pitagoras co związki w trójkącie 30 60 90 https://matematykaszkolna.pl/strona/2280.html
a potem AB2=12+(2−√3)2