 . Niestety pani profesor biegnie szybko do przodu aby nas wszystkiego nauczyć
i nie miała czasu aby z nami to dokładnie przerobić
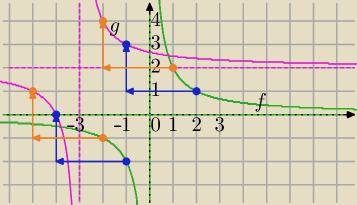
Zad. wykres funkcji określonej wzorem f(x)=2/x przesuń równolegle do osi odciętych ''w Lewo''
o 3 jednostki oraz równolegle do osi rzędnych ''w górę'' o 2 jednostki
a.) Określ wektor przesunięcia wykresu funkcji
b.) Napisz wzór funkcji, której wykres otrzymałeś i określ jej dziedzinę
c.) podaj równania asymptot otrzymanego wykresu
Z góry bardzo dziękuje nawet za drobną pomoc
. Niestety pani profesor biegnie szybko do przodu aby nas wszystkiego nauczyć
i nie miała czasu aby z nami to dokładnie przerobić
Zad. wykres funkcji określonej wzorem f(x)=2/x przesuń równolegle do osi odciętych ''w Lewo''
o 3 jednostki oraz równolegle do osi rzędnych ''w górę'' o 2 jednostki
a.) Określ wektor przesunięcia wykresu funkcji
b.) Napisz wzór funkcji, której wykres otrzymałeś i określ jej dziedzinę
c.) podaj równania asymptot otrzymanego wykresu
Z góry bardzo dziękuje nawet za drobną pomoc 
| 2 | ||
f(x)= | ||
| x |
| 2 | 2+2*(x+3) | 2x+8 | ||||
g(x)= | +2⇔ [g(x)= | ⇔g(x)= | ] | |||
| x+3 | x+3 | x+3 |