| 1 | 1 | ||
≤P(A)≤ | |||
| 6 | 4 |
 Na razie jestem zmuszony zostawic to .
Pozniej napisze do Ciebie
Na razie jestem zmuszony zostawic to .
Pozniej napisze do Ciebie
 na razie probuje to pojac .
na razie probuje to pojac .
 Dzień dobry!
Przed wyjaśnianiem rozwiązania tego typu zadań, dobrze sobie powtórzyć podstawowe prawa
rachunku zbiorów.
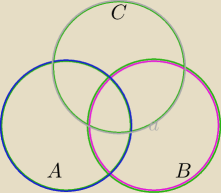
Wg mnie warto na diagramach Venna narysować sobie kilka praw. Zadanie nr 31 i to o które teraz
pytasz, też łatwiej będzie zrozumieć z rysunkami.
To bardzo przyda się też do rozwiązywania zadań z rachunku prawdopodobieństwa.
Spróbuj na takich diagramach rysować podstawowe prawa z tego zestawu
http://www.megamatma.pl/uczniowie/wzory/algebra-zbiorow/rachunek-zbiorow
narysuj na jednym diagramie np. (A∩B)' obok na drugim A'UB'.
Spróbuj też rozwiązać zadania od 14 ze strony 18. Nie musisz przeprowadzać formalnych dowodów,
Albo przekształcaj na podstawie twierdzeń, które znasz albo narysuj na diagramach
http://www.wzim.interblock.pl/Matematyka/Literatura/Banas_Wedrychowicz-Zbior_Zadan_z_Analizy_Matematycznej.pdf
Jeśli coś będzie niejasne, to pytaj.
Dzień dobry!
Przed wyjaśnianiem rozwiązania tego typu zadań, dobrze sobie powtórzyć podstawowe prawa
rachunku zbiorów.
Wg mnie warto na diagramach Venna narysować sobie kilka praw. Zadanie nr 31 i to o które teraz
pytasz, też łatwiej będzie zrozumieć z rysunkami.
To bardzo przyda się też do rozwiązywania zadań z rachunku prawdopodobieństwa.
Spróbuj na takich diagramach rysować podstawowe prawa z tego zestawu
http://www.megamatma.pl/uczniowie/wzory/algebra-zbiorow/rachunek-zbiorow
narysuj na jednym diagramie np. (A∩B)' obok na drugim A'UB'.
Spróbuj też rozwiązać zadania od 14 ze strony 18. Nie musisz przeprowadzać formalnych dowodów,
Albo przekształcaj na podstawie twierdzeń, które znasz albo narysuj na diagramach
http://www.wzim.interblock.pl/Matematyka/Literatura/Banas_Wedrychowicz-Zbior_Zadan_z_Analizy_Matematycznej.pdf
Jeśli coś będzie niejasne, to pytaj.