Prawdopodobienstwo Krzysiek60: Zadanie nr 31 Dowiesc ze P(AUBUC)= P(A)+P(B)+P(C)−P(A∩B)−P(B∩C)−P(A∩C)+P(A∩B∩C) Zadanie nr 32 od razu tutaj Dowiesc ze P(A−B)≥P(A)−P(B) Tych nie wiem jak zrobic nr 33 juz wiem .

iteRacj@: Witaj! Jakie wzory masz podane w podręczniku?

iteRacj@: 0≤P(A)≤1 dla każdego zdarzenia A ⊂ Ω P(Ω )=1 Ω – zdarzenie pewne P(∅)= 0 ∅ – zdarzenie niemożliwe (pusty podzbiór Ω ) P(A)≤P(B) gdy A⊂B⊂Ω P(A')=1− P(A), gdzie A′ oznacza zdarzenie przeciwne do zdarzenia A P(A∪B)= P(A)+P(B)−P(A∩B) dla dowolnych zdarzeń A, B ⊂ Ω P(A∪B)≤ P(A)+P(B) dla dowolnych zdarzeń A B, ⊂ Ω

Krzysiek60: https://zapodaj.net/66eb19fd19500.jpg.html https://zapodaj.net/527c981cb7bcb.jpg.html Dobry wieczor

Mila: P(A∪B)=P(A)+P(B)−P(A∩B) masz udowodnione str.39 L=P( (A∪B)+C)=P(A∪B)+P(C)−P((A∪B)∩C)= =P(A)+P(B)−P(A∩B) +P(C)− P((A∩C)∪(B∩C))= =P(A)+P(B)+P(C)−P(A∩B)−[P(A∩C)+P(B∩C))−P(A∩C∩B∩C)]= =P(A)+P(B)+P(C)−P(A∩B)−P(A∩C)−P(B∩C))+P(A∩B∩C)=P

iteRacj@: jeszcze taki warto znać P(A−B)=P(A)−P(A∩B)=P(A∩B') spróbuj tego skorzystać w zadaniu nr 32

Krzysiek60: Nie wiem .

iteRacj@: P(X)≤P(Y) gdy X⊂Y⊂Ω z tego twierdzenia wynika, że jesli zbiór X zawiera się w zbiorze Y, to prawdobodobieństwo zdarzenia P(X) jest mniejsze lub takie samo jak P(Y) u nas mamy rozważymy zbiory A∩B i B A∩B⊂B więc P(A∩B)≤P(B) a z tego −P(A∩B) ≥ −P(B) z tw. 19:45 wiemy że P(A−B)=P(A)−P(A∩B) ≥P(A)−P(B) c.b.d

Krzysiek60: Dzieki Wkurzaja mnie takie dowody i ich nie lubie No ale skoro sa takie zadania to nalezy sie z nimi chociaz zapoznac

iteRacj@: Mili dowód wygląda poważniej i budzi szacunek

Krzysiek60: Dlatego postaram sie go zrozumiec

iteRacj@: narysuj diagram koniecznie

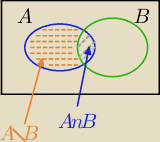
Mila: Zadanie nr 32 wykazać, że P(A−B)≥P(A)−P(B) P(A∩B)≤P(B) P(A\B)=P(A)−P(A∩B)≥P(A)−P(B)

Krzysiek60: Dziekuje CI bardzo Doslownie wszystko zapomnialem . Przeciez takie diagramy robilismy i prof. Hautmam tego pilnowal . Co sie dzieje

Krzysiek60: Byc moze ale kostke mama na tydzien

Krzysiek60: Zadanie nr 31 mam juz ogarniete (BUC) traktuje jako zbior B i A∩(BUC) =(A∩B)U(A∩C)