pochodne Aloha: https://matematykaszkolna.pl/forum/312895.html Czemu jedynki są pierwiastkami dwukrotnymi tutaj?

Basia: nie sa; x⁵(x⁴−1) = x⁵(x²−1)(x²+1) = (x−0)⁵(x−1)(x+1)(x²+1) 0 jest pierwiastkiem pieciokrotnym 1 i −1 to pierwiastki jednokrotne

Aloha: To znaczy, że funkcja pierwotna maleje mi od nieskonczonosci do jedynki i od zera do jedynki, a rosnie od −1 do 0 i od 1 do nieskonczonosci Jak mam udowodnić to, że funkcja pierwotna nie ma pierwiastków rzeczywistych skoro wiem ze i rosnie i maleje ,czyli teoretycznie moze przeciąć os iksów?

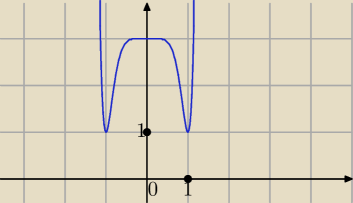
Janek191: Podany wielomian nie ma miejsc zerowych.

Aloha: A jak sprawdzić czy ma miejsca zerowe?

Basia: lim_x→±∞ W(x) = +∞ x∊(−∞;−1) ⇒ f'(x)<0 ⇒ f maleje x∊(−1,0) ⇒ f'(x)>0 ⇒ f rosnie x∊(0,1) ⇒ f'(x)<0 ⇒ f maleje x∊(1,+∞) ⇒ f'(x)>0 ⇒ f rosnie W(−1) = 3−5+3=1 W(0)=3 W(1)=3−5+3=1 wiec przebieg jest taki: w przedziale (−∞;−1> maleje od +∞ do 1 w przedziale <1;0> rosnie od 1 do 3 w przedziale <0;1> maleje od 3 do 1 w przedziale <1;+∞) rosnie od 1 do +∞ bo to wielomian czyli funkcja ciagla jej wartoscia najmniejsza jest 1, nie moze wiec byc rowna 0

Aloha: Dziękuję bardzo :3