POMOCY Andrzej : Jak rozwiazać nierówność z modułem po obu stronach Np. |x−4| ≥|x+2|−3

PW: Podobny przykład ze wskazówką: 369782

Jolanta: |x−4|=0 dla x=4 |x+2|=0 x=−2 przedziały (−∞.−2) <−2,4) <4,∞) 1) biorę np x=−3 −3−4=−7 przepraszam muszę odejsc

PW: Po powrocie przyznasz, że "biorę np. x=−3" to nienaukowa metoda. Tak zrozpaczone nauczycielki radzą swoim uczniom, ale chyba po to, żeby zamącić w głowach. I tak większa połowa nie rozumie po co to podstawienie.

Jolanta: wynik <0 czyli zmieniamy znaki −x+4 −3+2=−1 wynik<0 " " −x−2 −x+4≥−x−2−3 4>−5 x∊R v x∊(−∞,−2) x∊(−∞,−2) 2) x∊<−2,4) biorę np x=1 1−4<0 zmiana znaków −x+4 1+2>0 x+2 −x+4≥ x+2−3 5 ≥2x x ≤2,5 x∊ <−2; 2,5> 3) x∊<4,∞) biorę np x=5 5−4>0 x−4 5+2>0 x+2 x−4≥x+2 −4≥2 sprzeczne odp to suma odpowiedzi z 1) 2) 3) x∊(−∞,−2) v<−2 ,25> odp x∊(−∞,2,5)

Jolanta: Wiem,ale niektórym łatwiej to zrozumieć Dobrze,że jesteś .Możesz sprawdzic czy dobrze jest .Mam w domu male urwanie głowy

PW: Prawa strona może być ujemna: |x+2|−3<0 −3<x+2<3 −5<x<1 Widać więc, że wszystkie x∊(−5, 1) są rozwiązaniami zadanej nierówności (bo dla takich x lewa strona jest nieujemna, a prawa ujemna). Dla pozostałych x w nierówności |x−4| ≥|x+2|−3 obie strony są nieujemne, a więc po podniesieniu stronami do kwadratu dostajemy nierówność równoważną (x−4)²≥(x+2)²−6|x+2|+9, x∊R\(−5, 1) x²−8x+16≥x²−6|x+2|+9 6|x+2|≥8x−7, x∊(−∞, −5>∪<1, ∞). Znowu widać, że: − dla x∊(−∞, −5> prawa strona nierówności jest liczbą ujemną, a więc wszystkie te x są rozwiazaniami; − dla x∊<1, ∞) nierówność ma postać 6|(x+2)≥8x−7 6x+12≥8x−7 2x≤5

	5
x≤		,
	2

	5
rozwiązaniami są więc x∊<1,		>.
	2

	5		5
Odpowiedź: Rozwiązaniami są x∊(−5, 1)∪(−∞, −5>∪<1,		>, czyli x∊(−∞,		>.
	2		2

Odpowiedź ta sama, jedynie w ostatecznej wersji napisałaś przedział prawostronnie otwarty zamiast domkniętego.

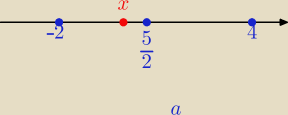
PW: Co najśmieszniejsze, całe te wysiłki można zastąpić jednym prostym rysunkiem z komentarzem:

	5
Dla x=		ma miejsce równość (to łatwo zgadnąć).
	2

	5
Dla x∊<−2,		) odległość od x do 4 zwiększa się, a odległość od x do −2 zmniejsza się −
	2

nierówność dalej jest prawdziwa. I tak dalej − można to rozwiązać graficznie komentując zachowanie się lewej i prawej strony w zależności od przemieszczania się x. Litera a pod rysunkiem jest chochlikiem, ale nie chce mi się już wracać, ciężko tu wykasować dowolny obiekt z rysunku.