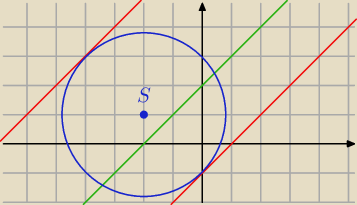
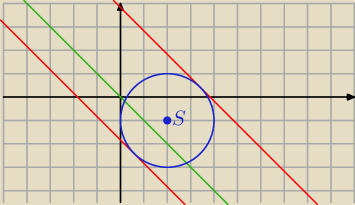
równania stycznych piotrek/liceum: Wyznacz równania stycznych do danego okręgu: a) x² + y² − 2x − 19 = 5, przechodzących przez punkt P(3,6) b) x² + y² + 4x − 2y − 3 = 0, równoległych do prostej x − y + 2 = 0 c) x² + y² + 2y − 12 = 0, prostopadłych do prostej 2x − 3y − 5 = 0 d) x² + y² − 4x + 2y + 1 = 0, nachylonych do osi OX pod kątem 135°

Janek191: b) x² + y² + 4 x − 2 y − 3 = 0 ( x + 2)² − 4 + (y − 1)² − 1 − 3 = 0 (x +2 )² + ( y − 1)² = 8 = (2√2)² S = ( − 2 , 1) r = 2√2 x − y + 2 = 0 ⇒ y = x + 2 Prosta równoległa y = x + k ⇒ x − y + k = 0 Odległość tej prostej od S = ( − 2, 1) jest równa r = 2√2 zatem

I 1*(−2) − 1*1 + k I
	= 2√2
√2

I − 3 + k I = 4 − 3 + k = − 4 lub − 3 + k = 4 k = −1 lub k = 7 Równania tych prostych stycznych: y = x − 1 y = x + 7

Eta: https://matematykaszkolna.pl/forum/367928.html

Janek191: ( x − 2)² + ( y + 1)² = 2² S = ( 2, − 1) r = 2 Prosta nachylona pod katem 135^o to y = − x + k inaczej x + y − k = 0 więc

I 1*2 + 1*(−1) − k I
	= 2
√2

I 1 − k I = 2√2 1 − k = −2√2 lub 1 − k = 2√2 k = 2√2 + 1 lub k = −2√2 + 1 Równania prostych stycznych: y = − x +2√2 + 1 y = − x −2 √2 + 1 =====================================

Janek191: Pozdrowienia dla ETY

piotrek/liceum: dziękuję

piotrek/liceum: pozdrowienia dla Ety i Janka191

Janek191: cd. do d) y = a x tg 135^o = − 1 = a więc y = − x Prosta równoległa to y = − x + k ma być styczna do okręgu.