7. Dany jest prostokąt ABCD o bokach długości |AB|= 2 i |BC|= p{3} oraz trójkąty
Alinka:
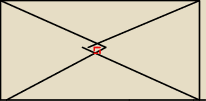
7. Dany jest prostokąt ABCD o bokach długości |AB|= 2 i |BC|=
√3 oraz trójkąty równoboczne
AED i BFC. Pole . Pole powierzchni zakreskowanej figury wynosi.
(wszystko na rysunku)
8. Dany jest okrąg o środku w punkcie O. Odległość srodka okręgu O od prostej k wynosi 3x−6,
zaś dł. Promienia tego okręgu jest równa 4x+2. Dla pewnych rzeczywistych wartości x.
Oblicz ile istnieje liczb rzeczywistych, dla których prosta k będzie styczna do okręgu.
Dla jakiego przedziału x k będzie sieczną tego okręgu.
Czy jest taka rzeczywista by prosta k zawierała średnicę.
25 sty 14:41
Alinka: up
26 sty 09:52
26 sty 11:10
Alinka:
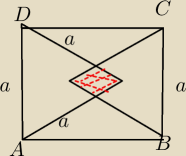
Zrobiłam i nadal nic ..
26 sty 15:25
===:
Ta zakreskowana figura to oczywiście romb o kącie ostrym 60o
... łatwo policzysz obie jego przekątne a więc i pole
Można oczywiście inaczej ... ze skali podobieństwa trójkątów
26 sty 16:19
===:
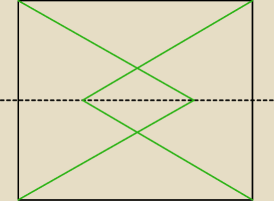
26 sty 16:33
Alinka: ale to ze to jest romb trzeba uzasaduc
26 sty 18:33
Mila:
Nie musisz, to czworokąt w którym przekątne są prostopadłe.
Obliczyłaś długości przekątnych?
26 sty 18:37
Alinka: tak 1 13 * √3 i 1
27 sty 18:24
Alinka: tylko muze sforuowac to ze skoro są prostopadłe to jest to romb a nie wiem jak, pomoze ktoś?
27 sty 18:25
27 sty 18:54
alinka: dziękuję ♥
27 sty 19:17
 7. Dany jest prostokąt ABCD o bokach długości |AB|= 2 i |BC|= √3 oraz trójkąty równoboczne
AED i BFC. Pole . Pole powierzchni zakreskowanej figury wynosi.
(wszystko na rysunku)
8. Dany jest okrąg o środku w punkcie O. Odległość srodka okręgu O od prostej k wynosi 3x−6,
zaś dł. Promienia tego okręgu jest równa 4x+2. Dla pewnych rzeczywistych wartości x.
Oblicz ile istnieje liczb rzeczywistych, dla których prosta k będzie styczna do okręgu.
Dla jakiego przedziału x k będzie sieczną tego okręgu.
Czy jest taka rzeczywista by prosta k zawierała średnicę.
7. Dany jest prostokąt ABCD o bokach długości |AB|= 2 i |BC|= √3 oraz trójkąty równoboczne
AED i BFC. Pole . Pole powierzchni zakreskowanej figury wynosi.
(wszystko na rysunku)
8. Dany jest okrąg o środku w punkcie O. Odległość srodka okręgu O od prostej k wynosi 3x−6,
zaś dł. Promienia tego okręgu jest równa 4x+2. Dla pewnych rzeczywistych wartości x.
Oblicz ile istnieje liczb rzeczywistych, dla których prosta k będzie styczna do okręgu.
Dla jakiego przedziału x k będzie sieczną tego okręgu.
Czy jest taka rzeczywista by prosta k zawierała średnicę.
 Zrobiłam i nadal nic ..
Zrobiłam i nadal nic ..
