 pomożecie
pomożecie Dany jest jest trójkąt równoramienny o ramieniu długości 6 cm i kącie przy podstawie 30 stopni.
Oblicz odległości punktu przecięcia prostych zawierających wysokości tego trójkąta od jego
wierzchołków.
Dany jest jest trójkąt równoramienny o ramieniu długości 6 cm i kącie przy podstawie 30 stopni.
Oblicz odległości punktu przecięcia prostych zawierających wysokości tego trójkąta od jego
wierzchołków.

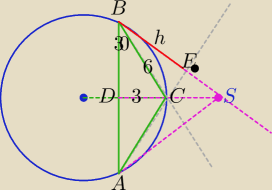 |DC|=3
|AB|=6√3
∡ABE=60o
ΔABS−Δrównoboczny
|BS|=|AS|=6√3
|DC|=3
|AB|=6√3
∡ABE=60o
ΔABS−Δrównoboczny
|BS|=|AS|=6√3
| 6√3*√3 | ||
|DS|= | =9 | |
| 2 |
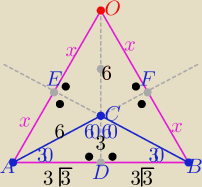 Punkt O przecięcia wysokości to ortocentrum trójkąta
Otrzymujemy sześć trójkątów przystających wykaż to......
zatem ΔABO jest trójkątem równobocznym o boku długości
|AB|=|AO|=|BO|= 6√3 i wysokości |DO|= 9 oraz |CO|=6
to są szukane odległości punktu O od wierzchołków
...........................
Punkt O przecięcia wysokości to ortocentrum trójkąta
Otrzymujemy sześć trójkątów przystających wykaż to......
zatem ΔABO jest trójkątem równobocznym o boku długości
|AB|=|AO|=|BO|= 6√3 i wysokości |DO|= 9 oraz |CO|=6
to są szukane odległości punktu O od wierzchołków
...........................

