aa olek: równanie prostej której tangens kata nachylenia do osi OX jest równy 2 oraz przechodzacej przez srodek odcinka o koncach a=(−2,−3) i b=(4,1) ma postać

5-latek: y=m(x−x₀)+y₀ m= tgα x₀ i y₀ to wsporzedne punktu przez ktory przechodzi prosta Przeciez masz wzory na wspolrzedne srodka odcinka wiec licz to akuratnie jest proste

olek: a to x i x₀ to jakie liczby?

5-latek: https://matematykaszkolna.pl/strona/1750.html

olek: i tak nie czaje

5-latek: Jesli nie potrafisz nawet podsatwic dio wzoru to twoj problem

the foxi: To może tak: środek odcinka to (1;−1) We wzorze funkcji liniowej y=ax+b a oznacza właśnie ten tangens kąta nachylenia, więc y=2x+b Podstaw do wzoru funkcji współrzędne tego środka, wyznacz b i napisz wzór funkcji.

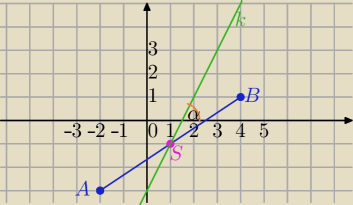
Mila: A=(−2,−3) i B=(4,1)

	−2+4		−3+1
S=(		,		)=(1,−1) środek AB
	2		2

y=ax+b, a=tgα y=2x+b i S∊prostej⇔−1=2*1+b⇔b=−3 k: y=2x−3 ========