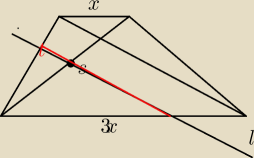
trapez k.b: Od czego zacząć W trapezie jedna z podstaw jest trzy razy dluższa od drugiej. Przez środek S jednej z przekątnych poprowadzono prostą l równoległą do drugiej przekatnej długości m. Wtedy długość odcinka prostej l zawartego wewnątrz trapezu jest równa: a) 3/2m b) 3/4m c) 2/3m d) 4/3mxx

k.b: Czy rysunek jest poprawny? i poprawka, odp d) 4/3m

iteRacj@: rysunek poprawny, −podstawy "wycinają" w trapezie dwa trójkąty stykajace się wierzchołakmi, są to trójkaty podobne w takiej skali, jak proporcja między długością podstaw −ta informacja pomoże znaleźć proporcję, w jakiej punkt przecięcia przekątnych dzieli krótszą przekątną i czerwony odcinek jest krótszy niż m, dwie odpowiedzi odpadają

Basia:

	a
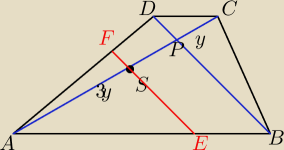
zacząć trzeba od tego, że w każdym trapezie trójkąty APB i CPD są podobne w skali k=
	b

u Ciebie k = 3 czyli PC=y i PA=3y natomiast PD = z i PB = 3z czyli 4z=m

	m
z =
	4

przekatna AC ma długość 4y czyli SC=2y i SA=2y

	AP		3y		3
z tego wynia, że trójkąty ADB i AFE w skali		=		=
	AS		2y		2

	2		2		m		m
czyli FS =		DP =		*		=
	3		3		4		6

	4
mogłam się gdzieś pomylić, ale na pewno nie jest to		m; przecież FS nie może być dłuższy
	3

od BD no chyba, że coś źle zrozumiałam

k.b: dziękuję bardzo za pomoc

Eta: https://matematykaszkolna.pl/forum/365333.html