trapez mat18: Dany jest trapez ABCD o polu 48, AB∥CD Przekątne tego trapezu przecinają się w punkcie E Pole trójkąta ABE jest równe 9 Wyznacz stosunek długości podstaw AB/CD

Eta: 1 sposób

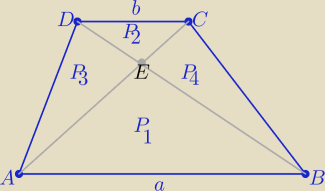
	a
Pole trapezu : P=(k+1)2*P2 , k=		−− skala podobieństwa trójkątów ABE i CDE
	b

P1		9
	=k2 ⇒ P2=
P2		k2

	9(k+1)2		3(k+1)		3
to		=48=16*3⇒		=4√3⇒		=4√3−3
	k2		k		k

	3		4√3+3
to k=		= .....=
	4√3−3		13

========== 2 sposób ........... jak wyżej

9		3
	=k2 ⇒ √P2=
P2		k

Pole trapezu wyraża się wzorem P=(√P₁+√P₂)²

	3		3
to (3+		)2=48=16*3 ⇒ 3+		=4√3 ⇒
	k		k

	4√3+3
k=........... =
	13

======= 3 sposób

	9
P3=P4=k*P2 , P1=k2*P2 ⇒ P2=
	k2

Pole trapezu: P= P₃+P₄+P₂+P₁ ⇒ 2kP₂+P₂= 39 ⇒ P₂(2k+1)=39 ⇒

9
	(2k+1)=39 /:3 ⇒ 13k2−6k−3=0 Δ=192 , √Δ=8√3 i k>0
k2

	6+8√3		4√3+3
k=		=
	26		13

=========

Eta: https://matematykaszkolna.pl/forum/237455.html Zajrzyj jeszcze tu.......