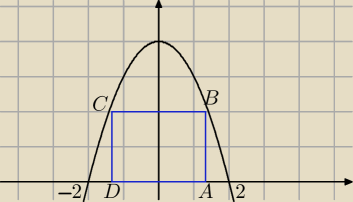
W parabolę o równaniu y = 4−x2 wpisano prostokąt, w sposób przedstawiony na rysunku.
Znaleźć wymiary prostokąta, który ma największe pole.
f(x)=4−x2=(2−x)(2+x),0)
A=(x,0) i 0<x<2
B=(x, 4−x2)
C=(−x, 4−x2)
D=(−x,0)
P − pole prostokąta ABCD
P = |AB|*|AD|
|AB| = |4−x2| = 4−x2
|AD| = |2x| =2x
P = (4−x2)*2x = −2x3+8x
f(x)= −2x3+8x
f'(x)= −6x2+8
| 2√3 | ||
funkcja f(x) dla x= | osiąga maksimum | |
| 3 |
| 2√3 | ||
stąd dla |AD| = 2 | ||
| 3 |
| 2√3 | 8 | |||
|AB| = 4−( | )2 = | |||
| 3 | 3 |