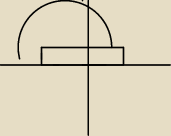
w parabolę o równaniu y=4-x^2 wpisano prostokąt quest: W parabolę o równaniu y = 4 − x² wpisano prostokąt, w sposób przedstawiony na rysunku. Znaleźć wymiary prostokąta, który ma największe pole.(sorry za rysunek ale nie ogarniam rysowania

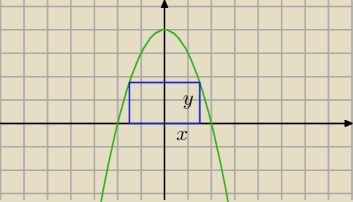
Jerzy: P = 2x*y = 2x(4 − x²) ... i szukasz maksimum.

quest: Wyszło mi maksimum (1,8) to dobrze?

Jerzy: Co to znaczy (1,8) ?

quest: f max Df x(1,8)

Jerzy: Jakie wymiary ma maksymalny prostokąt ?

quest: ja to wyliczyłem z monotoniczności pochodnych to chyba źle mam

Jerzy: Ty nie rozumiesz, co robisz. Pochodna zeruje si e dla: x = 1 , czyli dla x = 1 funkcja osiaga maksimum f(1) = 2*1*(4−1) = 6 Zatem prostokąt o maksymalny polu ma boki: a = 2x = 1 oraz b = y = 6

quest: To dobrze liczyłem to wyszło mi te x=1

Jerzy: Tylko nie potarfiłeś wyciągnąć wniosków.

quest: rozwiązanie złe, popełnili Panowie błędy przy liczeniu pochodnych. Poprawny wynik a=4/√3 i b=8/3

Jolanta: P=8x−2x³ Pochodna=8−6x² 6x²−8=0

	8
x2=
	6

	2
x=
	✓3

f(x)=4−x²

	4		2
f(2/✓3)=4−		=2
	3		3

.: Quest− pochodna to ty liczyłeś, a nie my. Fakt, faktem − nikt nie sprawdził czy dobrze policzyłeś, ale to już insza inszość.