równania
00000: Rozwiąż równanie: |x
2−4|+|x
2−5|=1. Jakie powinny być tutaj przedziały? Wychodzi mi:
1. (−
∞,−
√5> <
√5,+
∞)
2. (−
√5,−2> <2,
√5)
3. (−2,2)
poprawny wynik to:
<−
√5,−
√2> <2,
√5)
Mi z pierwszego przedziału wychodzi 2,5+
√5
cały drugi
i 0 z trzeciego
Mógłby ktoś mi wytłumaczyć jak to zrobić

?
10 gru 18:05
iteRacj@:
przedziały możesz zsumować, bo wartości bezwzględne "zachowują się" tak samo
1.(−∞,−√5> ∪ <−2,2> ∪ <√5,+∞)
2. (−√5,−2) ∪ (2, √5)
teraz zapisz jak będzie wyglądać równanie bez wartości bezwzględnej w obu przypadkach i rozwiąż
10 gru 18:21
Bogdan:
Przecież podobny przykład miałeś już wytłumaczony tu
363887
10 gru 18:35
00000: wiem i ten robię na podstawie tamtego, ale i tak mi nie wychodzi
10 gru 18:38
iteRacj@: mój błąd 18:05
przedziały masz dobre, powinny być trzy
1. (−∞,−√5> <√5,+∞)
2. (−√5,−2> <2,√5)
3. (−2,2)
10 gru 18:53
Mila:
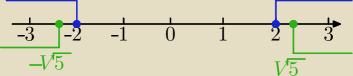 |x2−4|
|x2−4|+
|x2−5|=1
f(x)=x2−4 miejsca zerowe∊ {−2,2}
x
2−4≥0⇔x≤−2 lub x≥2
g(x)=x2−5 miejsca zerowe∊ {−
√5,
√5}
x
2−5≥0⇔x≤−
√5 lub x≥
√5
1) x≤−
√5 lub x≥
√5 obie funkcje przyjmują wartości nieujemne
x
2−4+x
2−5=1
2x
2=10
x
2=5 ⇔
x=√5 lub x=−√5
2) x∊(−
√5, −2>
x
2−4−x
2+5=1⇔1=1
Każda liczba
x∊(−√5, −2> spełnia równanie
3) x∊(−2, 2)
−x
2+4−x
2+5=1 ⇔
−2x
2=−8
x
2=4 ⇔x=2 lub x=−2 ∉D
4) x∊<2,
√5)
x
2−4−x
2+5=1
1=1
każda liczba x∊<2, √5) spełnia równanie
odp.
x∊<−
√5,−2> ∪<2,
√5>
10 gru 19:10
00000: Bardzo dziękuję, już rozumiem

Podziwiam, też chcę tak umieć matematykę

10 gru 20:03
Mila:

Na pewno to się uda, gdy włożysz trochę systematycznej pracy.
10 gru 20:08
PW: Trochę mnie nie było, więc może już niepotrzebnie, ale chcę podać rozwiązanie typu
"czary−mary", bez "rozbijania na przedziały".
Znana jest nierówność: dla dowolnych rzeczywistych a i b
|a+b| ≤ |a| + |b|,
przy czym równość ma miejsce wtedy i tylko wtedy, gdy co najmniej jedna z liczb jest równa zeru
lub a i b są tego samego znaku.
Biorąc
(1) a=x2−4, b = −5+x2
dostajemy:
1 = |(x2−4)+(−x2+5)| ≤ |x2−4| + |x2−5|,
czyli nierówność
1 ≤ |x2−4| + |x2−5|
jest spełniona dla wszystkich x, zaś równość
1 = |x2−4| + |x2−5|
ma miejsce wtedy i tylko wtedy, gdy jedna z liczb (1) jest zerem lub liczby te są jednakowych
znaków.
Rysujemy w jednym układzie współrzędnych wykresy funkcji
f(x) = x2−4 i g(x) = −5+x2
i odczytujemy zbiór rozwiązań (oczywiście taki jak końcowy u Mili).
11 gru 17:32
iteRacj@:
@PW mam pytanie, czemu w tym równaniu
1 = |(x2−4)+(−x2+5)| ≤ |x2−4| + |x2−5|
jest 1= |a−b| ≤ |a| + |b| (o ile dobrze to rozumiem)?
11 gru 19:01
PW: Tak, ale ja sobie "przekręciłem" : |x2−5|=|−x2+5| i wtedy korzystam z wzoru
1 = |a+b| ≤ |a|+|b|
11 gru 19:29
iteRacj@: dzięki za wyjaśnienie i za sposób : )
11 gru 20:23
PW: 
To:
364019 też by się tak dało.
11 gru 20:32
iteRacj@:
już to u siebie tak rozwiązuję, żeby przećwiczyć
11 gru 20:36
 ?
?
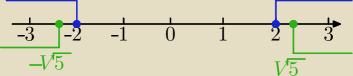 |x2−4|+|x2−5|=1
f(x)=x2−4 miejsca zerowe∊ {−2,2}
x2−4≥0⇔x≤−2 lub x≥2
g(x)=x2−5 miejsca zerowe∊ {−√5,√5}
x2−5≥0⇔x≤−√5 lub x≥√5
1) x≤−√5 lub x≥√5 obie funkcje przyjmują wartości nieujemne
x2−4+x2−5=1
2x2=10
x2=5 ⇔x=√5 lub x=−√5
2) x∊(−√5, −2>
x2−4−x2+5=1⇔1=1
Każda liczba x∊(−√5, −2> spełnia równanie
3) x∊(−2, 2)
−x2+4−x2+5=1 ⇔
−2x2=−8
x2=4 ⇔x=2 lub x=−2 ∉D
4) x∊<2, √5)
x2−4−x2+5=1
1=1 każda liczba x∊<2, √5) spełnia równanie
odp.
x∊<−√5,−2> ∪<2,√5>
|x2−4|+|x2−5|=1
f(x)=x2−4 miejsca zerowe∊ {−2,2}
x2−4≥0⇔x≤−2 lub x≥2
g(x)=x2−5 miejsca zerowe∊ {−√5,√5}
x2−5≥0⇔x≤−√5 lub x≥√5
1) x≤−√5 lub x≥√5 obie funkcje przyjmują wartości nieujemne
x2−4+x2−5=1
2x2=10
x2=5 ⇔x=√5 lub x=−√5
2) x∊(−√5, −2>
x2−4−x2+5=1⇔1=1
Każda liczba x∊(−√5, −2> spełnia równanie
3) x∊(−2, 2)
−x2+4−x2+5=1 ⇔
−2x2=−8
x2=4 ⇔x=2 lub x=−2 ∉D
4) x∊<2, √5)
x2−4−x2+5=1
1=1 każda liczba x∊<2, √5) spełnia równanie
odp.
x∊<−√5,−2> ∪<2,√5>
 Podziwiam, też chcę tak umieć matematykę
Podziwiam, też chcę tak umieć matematykę 
 Na pewno to się uda, gdy włożysz trochę systematycznej pracy.
Na pewno to się uda, gdy włożysz trochę systematycznej pracy.
 To: 364019 też by się tak dało.
To: 364019 też by się tak dało.