Prosze o pomoc
Kasia: Rozwiaz nierownosc.
D)|x+5|−|x−2|<=
E)|x+3|−|x−1|>1
30 lis 16:23
Kasia: Ed.D<=3
30 lis 16:23
30 lis 17:09
Kasia: Potrafie stworzyc przedzialy i znaki jakie wtedy moduly przyjmuja ale nie za bardzo wiem jak
dalej sie za to zabrać
30 lis 17:23
ite:
to zapisz, jakie masz przedziały, sprawdzę i powiem, co dalej
30 lis 18:02
Kasia: D = −∞;−5) (−5;2) (2;+∞)
E = (−∞;−3) (−3;1) (1;+∞)
30 lis 20:35
iteRacj@:
D/ zwróć uwagę że x∊ℛ, więc przedziały muszą uwzględniać wszystkie liczby rzeczywiste
i nie można −5 i 2 zgubić
czyli (−∞;−5), <−5;2), <2;+∞)
to samo w E
30 lis 20:49
Kasia: A no tak, a jak dalej do tego podejsc?
30 lis 21:06
Mila:
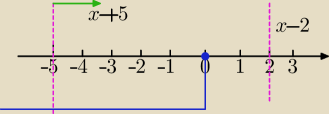
(*) |x+5|−|x−2|≤3
1) |x+5|=x+5 dla x≥−5
|x−2|=x−2 dla x≥2
a) x<−5
|x+5|=−x−5
|x−2|=−x+2 wtedy mamy nierówność:
−x−5−(−x+2)≤3
−x−5+x−2≤3
−7≤3 prawda⇔dla każdego x<−5 nierówność (*) jest spełniona
x∊(−∞,−5)
lub
b)x∊<−5,2)
|x+5|=x+5
|x−2|=−x+2⇔
x+5−(−x+2)≤3
x+5+x−2≤3
2x≤0
x≤0 i <−5,2)⇔
x∊<−5,0>
c) x≥2
x+5−(x−2)≤3
x+5−x+2≤3
7≤3 fałsz⇔ brak rozwiązań w tym przedziale
(a)lub (b) lub(c)
x∊(−∞,0>
30 lis 21:37
Kasia: Dziękuję Ci bardzo😊
30 lis 21:41
Mila:
Drugie rozwiąż w podobny sposób i napisz wynik.
30 lis 21:50
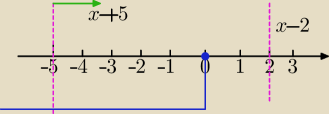 (*) |x+5|−|x−2|≤3
1) |x+5|=x+5 dla x≥−5
|x−2|=x−2 dla x≥2
a) x<−5
|x+5|=−x−5
|x−2|=−x+2 wtedy mamy nierówność:
−x−5−(−x+2)≤3
−x−5+x−2≤3
−7≤3 prawda⇔dla każdego x<−5 nierówność (*) jest spełniona
x∊(−∞,−5)
lub
b)x∊<−5,2)
|x+5|=x+5
|x−2|=−x+2⇔
x+5−(−x+2)≤3
x+5+x−2≤3
2x≤0
x≤0 i <−5,2)⇔
x∊<−5,0>
c) x≥2
x+5−(x−2)≤3
x+5−x+2≤3
7≤3 fałsz⇔ brak rozwiązań w tym przedziale
(a)lub (b) lub(c)
x∊(−∞,0>
(*) |x+5|−|x−2|≤3
1) |x+5|=x+5 dla x≥−5
|x−2|=x−2 dla x≥2
a) x<−5
|x+5|=−x−5
|x−2|=−x+2 wtedy mamy nierówność:
−x−5−(−x+2)≤3
−x−5+x−2≤3
−7≤3 prawda⇔dla każdego x<−5 nierówność (*) jest spełniona
x∊(−∞,−5)
lub
b)x∊<−5,2)
|x+5|=x+5
|x−2|=−x+2⇔
x+5−(−x+2)≤3
x+5+x−2≤3
2x≤0
x≤0 i <−5,2)⇔
x∊<−5,0>
c) x≥2
x+5−(x−2)≤3
x+5−x+2≤3
7≤3 fałsz⇔ brak rozwiązań w tym przedziale
(a)lub (b) lub(c)
x∊(−∞,0>