FUNKCJA HOMOGRAFICZNA: Punkt A(2,−3) jest środkiem symetrii wykresu funkcji homograficznej f(x)= (ax+12)/(cx+d). Wykres funkcji f przecina oś OY w punkcie o rzędnej −6. Oblicz współczynniki a, c, d. Wyznacz kąt nachylenia stycznej do wykresu funkcji f w punkcie o odciętej x0= 2 + pierwiastek z 6

Janek191:

	a x + 12
f(x) =
	c x + d

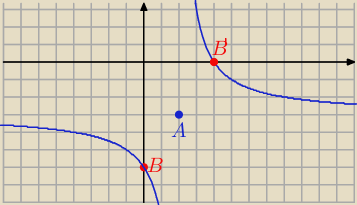
A = ( 2, −3) B = ( 0, − 6) ⇒ B' =( 4,0) więc

	12
f(0) =		= − 6 ⇒ d = − 2
	d

	4a + 12
f( 4) =		= 0 ⇒ a = − 3
	4 c + d

Mamy

	−3 x + 12
f(x) =
	c x − 2

	−3 x + 12
f(x) =
	x − 2

=======================

CZWOROKĄT: Rozumiem. Dzięki. A mogę prosić o ten kąt nachylenia stycznej?

5-latek: A to nie jest wartosc pochodnej w punkcie ?

CZWOROKĄT: No to jak obliczę pochodną, podstawię ten punkt to mi wyjdzie jakaś liczba. A skad mam wziąc kat nachylenia?>

CZWOROKĄT: POCHODNA: f'(x)= −6 / (x−2)² f'(2+pierwiastekz6) = −1 i co z tym?

Janek191:

	− 3*( x − 2) − ( −3 x + 12)*1		− 6
f '(x) =		=
	(x −2)2		(x −2)2

f '( 2 + √6) = − 1 = a = tg α α = 135^o ========= y = a x + b y = − x + b f( 2 + √6) = √6 − 3 zatem −2 − √6 + b = √6 − 3 ⇒ b = 2√6 − 1 y = − x + 2√6 − 1 =================

CZWOROKĄT: no ale kąt nachylenia stycznej wynosi 135? w jakim celu obliczyłeś dalej to: y = a x + b y = − x + b f( 2 + √6) = √6 − 3 zatem −2 − √6 + b = √6 − 3 ⇒ b = 2√6 − 1 y = − x + 2√6 − 1 ?

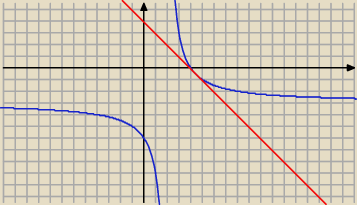
Janek191: Aby narysować tą styczną

5-latek: Napisal w gratisie rownanie tej stycznej

OBLICZ SUME: ale kat wynosi 135 mordko?

OBLICZ SUME: machniesz jeszcze to? : https://matematykaszkolna.pl/forum/362570.html