Monotoniczność funkcji Beata: Zbadać monotoniczność funkcji na podst. definicji. f(x)=2−(1/x)

Jerzy: Dziedzina: R\{0}

	−cxe−cx − e−cx		e−cx*(−cx − 1)
f'(x) =		=
	x2		x2

I teraz analizuj pochodną.

Jerzy: To nie do Ciebie

kochanus_niepospolitus: ale dziedzinę dobrze wyznaczyłeś

Jerzy: Gorzej z pochodną

kochanus_niepospolitus: oj tam oj tam Beato, czy znasz definicję

kochanus_niepospolitus: Analogiczne zadanie (nawet ten sam typ funkcji): https://matematykaszkolna.pl/forum/362499.html

Beata: Chciałam się upewnić co do wyniku

kochanus_niepospolitus: to podaj swój wynik, skoro już go masz

Beata: MAlejąca w przedziałach (−∞,0) oraz (0,∞) ?

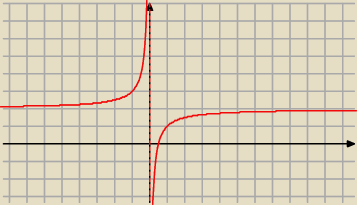
kochanus_niepospolitus: jak dla mnie to ona jest rosnąca

Adamm: ne jest rosnąca f(−1)>f(1) nie jest monotoniczna

Czarek: Kochanus miał chyba na myśli że jest rosnąca w przedziałach, poprawił Beatę poprostu i z tym się zgadzam funkcja rośnie w przedziałach x∊(−∞;0) i x∊(0;∞)

kochanus_niepospolitus: Adamm ... mój komentarz odnosił się do 15:32 i dotyczyło że nie jest ona malejąca w tych przedziałach tylko rosnąca w tych przedziałach