środkowe Kacper: Zadanko na wolne W trójkącie środkowe mają długość 30, 72 oraz 78. Oblicz pole tego trójkąta. Uwaga! Tylko rozwiązania na poziomie gimnazjum

PW: Czy 5²+12²=13²? Trochę zmniejszyłem ten trójkąt.

Kacper: Odpowiedź brzmi tak, ale skąd takie pytanie?

PW: A tak mi coś po głowie chodzi, że można łatwo zbudować trójkąt o bokach mających długości proporcjonalne do środkowych.

Mila: P_Δ=1440 ?

Eta: P=1440

Mariusz: Jeśli wykażemy że długość środkowej poprowadzonej z wierzchołka wynosi

	1
mA=		√2(b2+c2)−a2
	2

i analogicznie do pozostałych środkowych to dostaniemy układ równań nieliniowych (ale sprowadzalny do układu równań liniowych) Rozwiązujemy układ równań i stosujemy wzór Herona (bo on zawiera długości boków) Może istnieje jeszcze łatwiejsze rozwiązanie

PW: Jeszcze łatwiejsze? − To niemożliwe.

5-latek: Sposob latwiejszy Zagladamy do tablic matematyczno fizycznych np pod redakcja Wojtowicza z 1967r i tam na stronie 73 mamy taki wzor

	4
S=		√p'(p'−m1)(p'−m2)(p'−m3)
	3

	m1+m2+m3
gdzie p'=
	2

m₁ m₂ m₃ to dlugosci srodkowych

Eta: Trójkąt zbudowany ze środkowych : 30,72,78 jest prostokątny .... to jego pole S=1080

	4
P(ABC)=		S = ..=1440
	3

Mariusz: Nie wiem czy sposób który zaprezentowałem będzie akceptowalny bo jeśli chcielibyśmy uzasadnić wzory na długość środkowych to dla każdej środkowej musielibyśmy dwukrotnie skorzystać z wzoru cosinusów a wzoru cosinusów chyba nie ma w gimnazjum @Kacper trzeba uzasadniać wzór na długość środkowych czy można go wziąć z tablic czy skądś

Adamm: Eta dlaczego 4/3

Mariusz: Dla każdej środkowej musielibyśmy dwukrotnie skorzystać z wzoru cosinusów Dostaniemy układ równań nieliniowych (ale sprowadzalny do układu równań liniowych) Rozwiązujemy układ równań i stosujemy wzór Herona (bo występują w nim tylko długości boków) No właśnie sposób który ja przedstawiłem opiera się na powszechnie znanych wzorkach i jest zrozumiały nawet dla takiego sata ale nie wiem czy będzie akceptowalny bo w gimnazjum nie ma wzoru cosinusów Jednak sposób Ety wydaje się być ciekawy

Adamm: znalazłem coś takiego https://matematykaszkolna.pl/forum/52566.html ale jutro to przeczytam

Mariusz: Chyba to co znalazłeś powinno wystarczyć A więc jednak instnieje łatwiejszy sposób niż ten na który wpadłem

Eta:

	1
P(ABC)=		*4a*2h = 4ah
	2

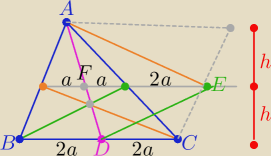
S(ADE) −−−Δ zbudowany ze środkowych

	1
ΔADE −− składa się z dwu trójkątów (AEF i DEF o równych polach S1=S2=		*3a*h
	2

to S= 3ah

P		4ah		4		4
	=		=		⇒ P(ABC)=		S
S		3ah		3		3

Eta: Ooooo To na darmo pisałam

Eta: Widzę,że tam też ja się udzielałam 7 lat temu

Mariusz: A teraz pytanie czy rozwiązanie które zaprezentowałaś jest w programie gimnazjum ? To rozwiązanie do którego doszedłem czyli 1. Wzory cosinusów (do znalezienia wzorów na długości środkowych) 2. Układ równań nieliniowych sprowadzalny do układu równań liniowych (do znalezienia długości boków) 3. Wzór Herona (do obliczenia pola mając dane długości boków) też wygląda dość zrozumiale jednak w tej postaci korzysta z twierdzeń czy wzorków którch gimnazjaliści mogą nie znać Gdyby wzory cosinusów zastąpić twierdzeniem Pitagorasa a układ równań rozwiązywać nie korzystając z odwracania i mnożenia macierzy tylko podstawianiem to sposób mógłby być akceptowalny

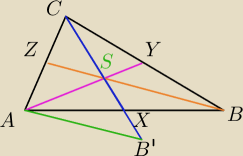
Kacper: Rozwiązanie Ety bardzo fajne Ja mam trochę inne. Wszystkie 6 trójkątów mają pola równe (łatwe do pokazania) Odłóżmy odcinek XB' o długości SX.

	1
Zatem ΔAB'X ≡ ΔBSX, zatem PASB'=		PABC
	3

Jak dodamy dane, to się okaże, że ΔAB'S jest prostokątny i zadanko robi się ładnie.

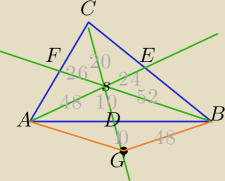
Mila: 1) |DG|=|DS| Czworokąt AGBS− równoległobok 2) P_ΔSGB: p=10+24+26=60 Z wzoru Herona : P_ΔSGB=480 480:2=240 P_ΔABC=6*240=1440

Eta: Hej Mila W gimnazjum uczą obliczania pola ze wzoru Herona ?

Mila: Uczą.

wiesiu: Ja nie sądzę Chyba że na jakiś kółkach

Mariusz: Jeszcze nie tak dawno trygonometria była w podstawówce (ostatnie lata gdy podstawówka była ośmioletnia) Co do wzoru Herona to nie pamiętam ale chyba też był Czyżby aż tak obniżyli poziom nauczania ? Ludzie z forum pisali że wyrzucili z liceum całą analizę i znaczną część algebry Jeśli chodzi o analizę to jeszcze niedawno wszystko do całek pojedynczych włącznie − nieoznaczone , oznaczone ,niewłaściwe było w liceum bądź w technikum Jeśli chodzi o algebrę liniową to były np wyznaczniki zastosowania wyznaczników do rozwiązywania układów równań liniowych (odpuszczono jednak dokładne sprawdzanie czy układ jest sprzeczny czy nieoznaczony ) Wyznaczniki były stosowane też do obliczenia pól i objętości w analizie mamy do tego całki W podstawówce były na pewno wzory skróconego mnożenia twierdzenie Pitagorasa i Talesa (twierdzenie Pitagorasa pociąga za sobą podobieństwo) trygonometria wiesiu skąd takie przypuszczenie ? Chodzisz do gimnazjum czy co ?