 wydaje mi się, że P=0,5, ale to za łatwe.
wydaje mi się, że P=0,5, ale to za łatwe.  pewnie się mylę
pewnie się mylę
| 3 | |
? jeśli to poprawna odpowiedz, to przedstawię obliczenia | |
| 4 |


| 3 | ||
no mi wyszło | , ale podejrzewam, że to dlatego, że źle zinterpretowałem to zadanie, więc | |
| 4 |

| 3 | ||
Przedstaw Amaz swoje obliczenia, bo wynik | jest poprawny. | |
| 4 |
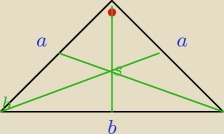 W treści zadania nie jest napisane jaki to ma być trójkąt, więc według założenia zadania, taki
sam wynik bedzie dla kazdego trójkąta. Bez straty ogólności możemy wybrać sobie KONKRETNY
trójkąt, który bedzie dla nas wygodny.
Takim trójkątem bedzie trójkąt, który jest zarazem prostokątny i równoramienny, jego pole równe
jest 1.
W treści zadania nie jest napisane jaki to ma być trójkąt, więc według założenia zadania, taki
sam wynik bedzie dla kazdego trójkąta. Bez straty ogólności możemy wybrać sobie KONKRETNY
trójkąt, który bedzie dla nas wygodny.
Takim trójkątem bedzie trójkąt, który jest zarazem prostokątny i równoramienny, jego pole równe
jest 1.
| a2 | ||
P=1= | ⇒ a=√2, b=2 | |
| 2 |
| √10 | ||
s2=s3= | ||
| 2 |
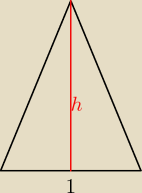 No to teraz tworzymy trójkąt równoramienny zbudowany z środkowych.
No to teraz tworzymy trójkąt równoramienny zbudowany z środkowych.
| √10 | ||
Ramię tego trójkąta ma długość | ||
| 2 |
| 3 | ||
Z tw.Pitagorasa h= | ||
| 2 |
| 1 | 3 | 3 | ||||
Pole trójkąta zbodowanego z środkowych jest równe: P=1* | * | = | ||||
| 2 | 2 | 4 |
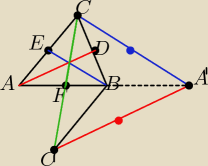 P −−− pole trójkąta ABC
P1 −−− pole trójkąta zbudowanego ze środkowych
ΔA'C'C −−− zbudowany z podwojonych środkowych ( na rys. z tw. odwrotnego do tw. Talesa
zatem
P(ΔA'C'C) = 4 P1 ( bo są podobne w skali k= 2
ΔA'C'C składa się z trójkątów : BC'A' , BCC' , BCA'
trójkąty te mają równe pola = polu Δ ABC
bo:
IBA'I= IABI i hAB−− tej samej długości
środkowa CF dzieli ΔABC na dwa trójkąaty o równych polach
zatem P(ΔCBC')= P(ΔABC)
czyli:
P(ΔA'C'C) = 3P( ΔABC)= 3P ( z oznaczenia
P −−− pole trójkąta ABC
P1 −−− pole trójkąta zbudowanego ze środkowych
ΔA'C'C −−− zbudowany z podwojonych środkowych ( na rys. z tw. odwrotnego do tw. Talesa
zatem
P(ΔA'C'C) = 4 P1 ( bo są podobne w skali k= 2
ΔA'C'C składa się z trójkątów : BC'A' , BCC' , BCA'
trójkąty te mają równe pola = polu Δ ABC
bo:
IBA'I= IABI i hAB−− tej samej długości
środkowa CF dzieli ΔABC na dwa trójkąaty o równych polach
zatem P(ΔCBC')= P(ΔABC)
czyli:
P(ΔA'C'C) = 3P( ΔABC)= 3P ( z oznaczenia
| 3 | ||
to: 4P1= 3P => P1= | P
| |
| 4 |

 czy takie rozwiązanie uznasz za poprawne ? .....
czy takie rozwiązanie uznasz za poprawne ? .....  czy przedstawisz ( jak zwykle ) jakiś inny , prostszy sposób .
Pozdrawiam
czy przedstawisz ( jak zwykle ) jakiś inny , prostszy sposób .
Pozdrawiam
 Ja rozwiązałem to zadanie nieco inaczej, pokażę za chwilę to rozwiązanie.
Warto problem pokazany w tym zadaniu pociągnąć dalej i budować w ten sam sposób
kolejne trójkąty. Każdy trójkąt za wyjątkiem pierwszego jest zbudowany ze środkowych
poprzedniego trójkąta. Jakie pola powierzchni mają kolejne trójkąty, jeśli pierwszy trójkąt ma
pole równe P, jaki ciąg tworzą liczby równe polom powierzchni kolejnych trójkątów. Jaka
zależność wiąże ze sobą długości boków co drugiego trójkąta?
Ja rozwiązałem to zadanie nieco inaczej, pokażę za chwilę to rozwiązanie.
Warto problem pokazany w tym zadaniu pociągnąć dalej i budować w ten sam sposób
kolejne trójkąty. Każdy trójkąt za wyjątkiem pierwszego jest zbudowany ze środkowych
poprzedniego trójkąta. Jakie pola powierzchni mają kolejne trójkąty, jeśli pierwszy trójkąt ma
pole równe P, jaki ciąg tworzą liczby równe polom powierzchni kolejnych trójkątów. Jaka
zależność wiąże ze sobą długości boków co drugiego trójkąta?
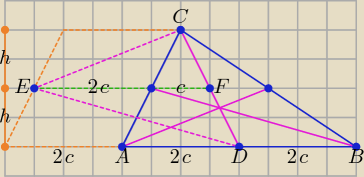 Mam nadzieję, że rysunek jest zrozumiały.
Mam nadzieję, że rysunek jest zrozumiały.
| 1 | ||
Pole trójkąta ABC (niebieskiego): P1 = | * 4c * 2h = 4ch | |
| 2 |
| 1 | 1 | 1 | 3 | |||||
P2 = | * 3c * h + | * 3c * h = 2 * | * 3c * h = 3ch = | * 4ch, | ||||
| 2 | 2 | 2 | 4 |
| 3 | ||
a więc P2 = | P1. | |
| 4 |
| 3 | ||
Jeśli P1 = 1, to P2 = | ||
| 4 |
 Dobranoc
Dobranoc 