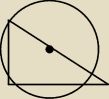
 Oblicz pole koła opisanego na trójkącie prostokątnym, w którym jedna przyprostokątna jest o 2
dłuższa od drugiej a pole trójkata wynosi 24
Witam, mam problem z tym zadaniem ponieważ utknąłem w połowie rozwiązania,
sporządziłem juz rysunek oraz zapis, że krótsza przyprostokątna jest równa x
a dłuższa przyprostokątna natomiast x + 2
Obliczyłem X z pola trójkąta zamieniając h = b (nie wiem, czy do końca tak mogę zrobić)
widziałem na internecie w którymś z zadań, że to możliwe.
Wyszło mi więc, że 24 = 1/2 a * b
24 = x + 2 * x / 2
z czego wyszło mi, że x = 16
Więc x + 2 = 18.
Zastosowałem twierdzenie pitagorasa by obliczyć przeciwprostokątną i wyszło mi 162 + 182 =
c2
256 + 324 = c2 i wychodzi niestety nieprzyjemna sytuacja z pierwiastkiem.
Ma ktoś inny pomysł lub może skorygować mój? będę bardzo wdzięczny, pozdrawiam!
Oblicz pole koła opisanego na trójkącie prostokątnym, w którym jedna przyprostokątna jest o 2
dłuższa od drugiej a pole trójkata wynosi 24
Witam, mam problem z tym zadaniem ponieważ utknąłem w połowie rozwiązania,
sporządziłem juz rysunek oraz zapis, że krótsza przyprostokątna jest równa x
a dłuższa przyprostokątna natomiast x + 2
Obliczyłem X z pola trójkąta zamieniając h = b (nie wiem, czy do końca tak mogę zrobić)
widziałem na internecie w którymś z zadań, że to możliwe.
Wyszło mi więc, że 24 = 1/2 a * b
24 = x + 2 * x / 2
z czego wyszło mi, że x = 16
Więc x + 2 = 18.
Zastosowałem twierdzenie pitagorasa by obliczyć przeciwprostokątną i wyszło mi 162 + 182 =
c2
256 + 324 = c2 i wychodzi niestety nieprzyjemna sytuacja z pierwiastkiem.
Ma ktoś inny pomysł lub może skorygować mój? będę bardzo wdzięczny, pozdrawiam!
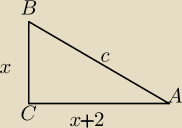 c>x+2
x>0
1)
c>x+2
x>0
1)
| 1 | |
*x*(x+2)=24 | |
| 2 |
| −2−14 | ||
x= | <0 lub x=6 | |
| 2 |
 , ma ktoś jeszcze chwilkę czasu zerknąć na jedno
zadanie? Wiem tylko tyle, że prawdopodobnie trzeba zastosować tu twierdzenie sinusów
ale nie do końca wiem w jaki sposób obliczyć miary kąta w momencie, gdy mam podane
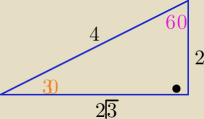
a = 2
b = 2√3
c = 4
, ma ktoś jeszcze chwilkę czasu zerknąć na jedno
zadanie? Wiem tylko tyle, że prawdopodobnie trzeba zastosować tu twierdzenie sinusów
ale nie do końca wiem w jaki sposób obliczyć miary kąta w momencie, gdy mam podane
a = 2
b = 2√3
c = 4
| a*b*c | ||
R= | ||
| 4P |
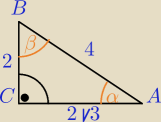 1) sprawdzamy, czy trójkąt jest prostokątny
42=16 − kwadrat dł. najdłuższego boku
22+(2√3)2=4+4*3=16 − suma kwadratów długości krótszych boków
16=16 ⇔trójkąt jest prostokątny
∡C=90o
1) sprawdzamy, czy trójkąt jest prostokątny
42=16 − kwadrat dł. najdłuższego boku
22+(2√3)2=4+4*3=16 − suma kwadratów długości krótszych boków
16=16 ⇔trójkąt jest prostokątny
∡C=90o
| 2 | 1 | √3 | ||||
tgα= | = | = | ⇔ | |||
| 2√3 | √3 | 3 |
 No to teraz masz wyjasnione .
No to teraz masz wyjasnione .

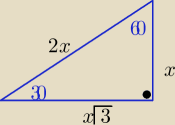 1/ sprawdzamy czy trójkąt jest prostokątny
22+(2√3)2=42 ⇒ 16=16 −− więc jest prostokątny
1/ sprawdzamy czy trójkąt jest prostokątny
22+(2√3)2=42 ⇒ 16=16 −− więc jest prostokątny
| 2 | 1 | |||
sinα= | = | ⇒ α= 30o to β= 60o | ||
| 4 | 2 |


