Analiza Mariusz: Wykazać, że wśród prostokątów wpisanych w trójkąt równoboczny o boku a>0 istniej taki, który ma największe pole. Znaleźć to pole. Od czego zacząć jak to ugryźć ? Za każdą pomoc będę wdzięczny zadanie znajdę się w temacie o funkcjach ciągłych więc na pewno jest to jakoś powiązane.

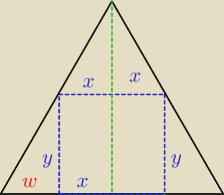
kochanus_niepospolitus: P = (2x)*(2y) y = √3w ; a = x+w −> y = √3(a−x) Czyli: P = (2x)*(2√3(a−x)) ; gdzie 'a' to stała P = 4√3x*(a−x)

	0+a		a
Maximum ta parabola osiąga dla x =		=
	2		2

	a
PMax = 4√3*(		)2 = a2√3
	2

Mariusz: Dziękuje bardzo

kochanus_niepospolitus:

	a
uwaga ... błąd popełniłem ... 'moje a' to tak naprawdę
	2

Eta: https://matematykaszkolna.pl/forum/360600.html I tu też................ Za dużo było ......