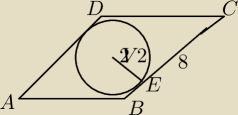
okrąg wpisany w romb jurek: Promień okręgu wpisanego w romb ABCD jest równy 2√2. Odcinek CE ma długość 8. Oblicz pole rombu.

Janek191: O − środek okręgu x = I OC I Mamy x² = (2√2)² + 8² = 8 + 64 = 72 = 36*2 x = 6√2 zatem I AC I = 2 x = 12 √2 oraz I BD I = 2*2√2 = 4 √2 Pole rombu P = 0,5 I AC I * I BD I = 0,5*12√2*4√2 = 48 [ j²] ========================================

Janek191: Źle − coś mnie zaćmiło.

Janek191: Niech I BE I = y 8 y = (2p{2])² = 8 y = 1 I BO I² = 1² + (2p{2])² = 1 + 8 = 9 I BO I = 3 Pole rombu P = 0,5*( 2*6√2)*6 = 36√2 [ j²] =============================

Eta: https://matematykaszkolna.pl/forum/360299.html