| I 4 x − 3 y + 13 I | 12 | ||
= | |||
| 5 | 5 |
 A(a,b)
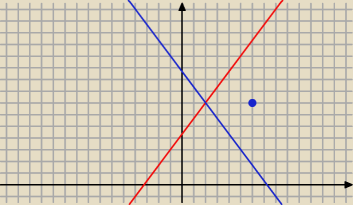
Proste przecinają się, nie są prostopadłe (4*4−3*3≠0)
Punkt A leży na dwusiecznej kąta między prostymi.
1) punkt przecięcia prostych
k: 4x−3y+13=0 i
m: 4x+3y−29=0
−−−−−−−−−−−−−− +
8x=16
x=2, y=7
S=(2,7)
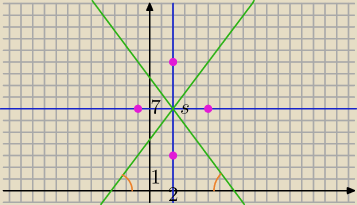
2) dwusieczna −zbiór punktów jednakowo odległych od ramion kąta,
otrzymamy równania dwóch dwusiecznych
P(x,y) − dowolny punkt dwusiecznej
Obie dwusieczne przechodzą przez punkt S, są do siebie prostopadłe⇔
A(a,b)
Proste przecinają się, nie są prostopadłe (4*4−3*3≠0)
Punkt A leży na dwusiecznej kąta między prostymi.
1) punkt przecięcia prostych
k: 4x−3y+13=0 i
m: 4x+3y−29=0
−−−−−−−−−−−−−− +
8x=16
x=2, y=7
S=(2,7)
2) dwusieczna −zbiór punktów jednakowo odległych od ramion kąta,
otrzymamy równania dwóch dwusiecznych
P(x,y) − dowolny punkt dwusiecznej
Obie dwusieczne przechodzą przez punkt S, są do siebie prostopadłe⇔
| 4 | 13 | |||
y= | x+ | |||
| 3 | 3 |
| 4 | 29 | |||
y=− | x+ | |||
| 3 | 3 |
| 4 | 4 | |||
tgα= | i tgβ=− | ⇒ | ||
| 3 | 3 |
| 12 | 4x0−3*7+13| | |||
d(A(x0,7),k)= | = | |||
| 5 | √42+32 |
| 12 | |
*5=|4x0−8| | |
| 5 |
| 12 | |4*2−3*y0+13| | |||
d(A(2,y0),k)= | = | |||
| 5 | √42+32 |