MalWas: Udowodnij, że jeśli środki ramion trapezu połączymy odcinkiem to jest on równoległy

	a+b
do podstaw a i b oraz równy		.
	2

karty do gry : Średnia arytmetyczna.

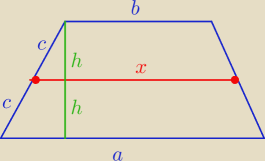Janek191: Z tw. Talesa wynika, że odcinek o długości x jest równoległy do podstaw trapezu. Mamy 0,5 ( a + x )*h + 0,5 ( b + x)*h = 0,5 ( a + b)*2 h / *2 (a + x)*h + ( b + x)*h = ( a + b)² h / : h a + x + b + x = 2*(a + b) 2 x = 2 a + 2 b − a − b 2 x = a + b / : 2

	a + b
x =
	2

================

MalWas: A jak udowodnić, że odcinek x jest równoległy do podstaw trapezu? Mógłby ktoś to zapisać skąd to się bierze...

PW: Uzasadnieniem równoległości jest twierdzenie odwrotne do twierdzenia Talesa. Trzeba zobaczyć ramiona kąta, na których dwie proste wyznaczają odcinki tak samo proporcjonalne.

MalWas: Z racji tego, że ja tego nie widzę to prosiłabym o rozpisanie

PW: Najpierw, korzystając z tej podpowiedzi, udowodnij to: 360147

Mila: Jeżeli proste przecinające ramiona kąta wyznaczają na jednym ramieniu odcinki proporcjonalne do odpowiednich odcinków na drugim ramieniu to te proste są równoległe.

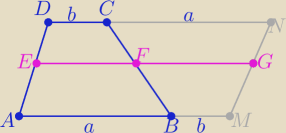Eta: Tak narysowany czworokąt jest równoległobokiem

	a+b
|EG|=a+b to |EF|=
	2

i EF∥AB ∥DC

MalWas:

	a+b
Napisałaś tak od razu że EG=a+b oraz EF=
	2

Skąd to się tak od razu wzięło

Jerzy: Nie wdzisz tego na rysunku ?

lolo: eta sam rysunek to za mało...

5-latek: Rysunek i dowod masz w ksiazce wiec w czym problem ?

MalWas: w jakiej książce?

Adamm: rysunek, z dobrym komentarzem nie trzeba być geniuszem by zrozumieć co przekazuje nam rysunek Ety, a przekazuje dużo

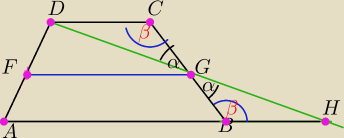
5-latek: Czesc Adamm albo taki FG linia srodkowa Dla dowodu wykreslimy z punktu D przez G prosta ktora prztnie przdluznie AB w punkcie H Trojkaty DGC i GBH sa przystajace bo DG= GH z zalozenia katy α rowne jako wierzcjholkowe katy β rowne jako naprzemianlegle wewnetrzne stad CD= BH Zateem AH= AB+CD Teraz popatrz na trojkat ADH i powiedz czym jest dla tego trojkata FG ? czemu jest rowny ? (poprzedni post Wniosek ?

5-latek: Popraw sobie CG = GB z zalozenia (popatrzylem nie na te odcinki

Adamm: Cześć

MalWas: Czy ktoś mógłby troszkę bardziej rozpisać metodę i rozwiązanie, które zamieściła Eta?

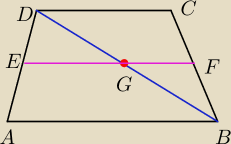PW: Przez punkt F prowadzimy prostą równoległą do AB. Prosta ta przecina przekątną BD w pewnym punkcie G. Z twierdzenia Talesa wynika, że G dzieli przekątną na połowy. Patrzymy teraz na kąt DBC. Jego ramiona zostały przecięte prostą GF w ten sposób, że odcinki GB i GD oraz FB i FC są tak samo proporcjonalne (są akurat równe, bo G dzieli BD na pól i F dzieli BC na pół). Na podstawie twierdzenia odwrotnego do twierdzenia Taleda prosta FG jest równoległa do DC. Ponieważ DC||AB, a relacja równoległości jest przechodnia, więc również GF||AB.. Pokazaliśmy, że przez punkt G przechodzą proste EG i GF, obie równoległe do AB. Zgodnie z piątym postulatem Euklidesa proste te pokrywają się (przez punkt G nienależący do AB przechodzi tylko jedna równoległa do AB), czyli EF||AB. A podpowiadałem, pani MalWas.

PW: Korekta: Talesa, nie Taleda. Przepraszam, mistrzu, to sąsiednie klawisze.

PW: I w pierwszym zdaniu: Przez punkt E prowadzimy prostą równoległą do AB.