| a+b | ||
do boku c i równy | . | |
| 2 |
 Twierdzenie (proste )
jesli na jednym ramieniu kata odlozymy kilka rownych odcinkow i przez [punkty podzialu
wykreslimy proste do siebie rownolegle
to te proste wyznacza na drugim ramieniu kata odcinki rowne miedzy soba
Dowod tego twierdzenia masz w ksiazce
Twierdzenie odwrotne
Jezeli na kazdym ramieniu kata odlozymy po kilka odcinkow tak aby te odcinki odkladane na tym
samyn ranieniu byly rowne miedzy soba to proste przechodzace przez kolejne punkty podzialu
obu ramiaon beda do siebie rownolegle
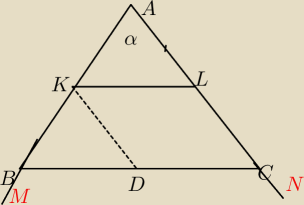
Na ramieniu AM kata α odkladamy dwa odcinki rowne AK= KB i przez punkty K i B wykreslamy
proste KL i BC do siebie rownolegle
Zgodnie z teirdzeniem prostym odcinki AL i LC beda sobie rowne
Otrzymales jednoczesnie trojkat ABC w ktorym odcinek KL przechodzacy przez srodek boku AB
jest rownolegly do boku BC i dzieli bok AC na polowy
Wiec twierdzenie proste moze byc wypowiedzane tak w przypadku trojkata
Twierdzenie : Jezeli przez srodek jednego boku trojkata wykreslimy rownolegla do boku
drugiego to podzeli ona trzeci bok na polowy
jesli zmienimy nasze zalozenie i przyjmiemy ze na ramieniu AM kąta α odlozymy dwa rowne
odcinki AK=KB a na ramieniu AN odlozylismy dwa rowne miedzy soba odcinki AL=LC po czym
punkty K i L oraz BiC polaczymy odcinkami KL i BC
TO zalozenie odpowiada teraz dokladnie twierdzeniu odwrotnemu
Stad na podsatwie tego twierdzenia dochodzimy do wnoisku iz w trojkacie ABC odcinek KL
laczacy srodki bokow AB i AC jest rownolegly do boku BC
Teraz udowodnimy ze odcinek KL jest rowny polowie boku AC
Kreslimy z punktu K odcinek KD rownolegly do boku AC i zwroc uwage na ytrojkat ABC
Odcinek KD wykreslony zostal przez srodek boku BA rownolegle do boku AC wiec zgodnie z tym co
wyzej podzielil bok BC na polowy
atad DB= DC
Odcinek DC jest rowny odcinkowi KL jako przeciwlwgle boki rownolegloboku KLDC wiec KL=DC
Twierdzenie (proste )
jesli na jednym ramieniu kata odlozymy kilka rownych odcinkow i przez [punkty podzialu
wykreslimy proste do siebie rownolegle
to te proste wyznacza na drugim ramieniu kata odcinki rowne miedzy soba
Dowod tego twierdzenia masz w ksiazce
Twierdzenie odwrotne
Jezeli na kazdym ramieniu kata odlozymy po kilka odcinkow tak aby te odcinki odkladane na tym
samyn ranieniu byly rowne miedzy soba to proste przechodzace przez kolejne punkty podzialu
obu ramiaon beda do siebie rownolegle
Na ramieniu AM kata α odkladamy dwa odcinki rowne AK= KB i przez punkty K i B wykreslamy
proste KL i BC do siebie rownolegle
Zgodnie z teirdzeniem prostym odcinki AL i LC beda sobie rowne
Otrzymales jednoczesnie trojkat ABC w ktorym odcinek KL przechodzacy przez srodek boku AB
jest rownolegly do boku BC i dzieli bok AC na polowy
Wiec twierdzenie proste moze byc wypowiedzane tak w przypadku trojkata
Twierdzenie : Jezeli przez srodek jednego boku trojkata wykreslimy rownolegla do boku
drugiego to podzeli ona trzeci bok na polowy
jesli zmienimy nasze zalozenie i przyjmiemy ze na ramieniu AM kąta α odlozymy dwa rowne
odcinki AK=KB a na ramieniu AN odlozylismy dwa rowne miedzy soba odcinki AL=LC po czym
punkty K i L oraz BiC polaczymy odcinkami KL i BC
TO zalozenie odpowiada teraz dokladnie twierdzeniu odwrotnemu
Stad na podsatwie tego twierdzenia dochodzimy do wnoisku iz w trojkacie ABC odcinek KL
laczacy srodki bokow AB i AC jest rownolegly do boku BC
Teraz udowodnimy ze odcinek KL jest rowny polowie boku AC
Kreslimy z punktu K odcinek KD rownolegly do boku AC i zwroc uwage na ytrojkat ABC
Odcinek KD wykreslony zostal przez srodek boku BA rownolegle do boku AC wiec zgodnie z tym co
wyzej podzielil bok BC na polowy
atad DB= DC
Odcinek DC jest rowny odcinkowi KL jako przeciwlwgle boki rownolegloboku KLDC wiec KL=DC
| 1 | ||
stad wnosisz a ze KL= | BC | |
| 2 |
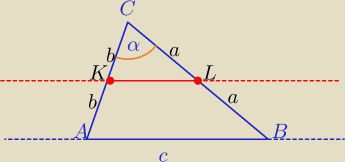 AC=2b, BC=2a, AB=c
1)
Z Tw. odwrotnego do tw. Talesa:
Jeżeli proste przecinające ramiona kąta wyznaczają na jednym ramieniu odcinki proporcjonalne
do odpowiednich odcinków na drugim ramieniu to dwie proste są równoległe.
AC=2b, BC=2a, AB=c
1)
Z Tw. odwrotnego do tw. Talesa:
Jeżeli proste przecinające ramiona kąta wyznaczają na jednym ramieniu odcinki proporcjonalne
do odpowiednich odcinków na drugim ramieniu to dwie proste są równoległe.
| a | a | a | b | ||||
= | ⇔ | = | =1 | ||||
| b | b | a | b |
| b | 2b | ||
= | |||
| |KL| | |AB| |
| 1 | ||
|KL|= | c | |
| 2 |
