trapez
Jupi: Oblicz pole trapezu o podstawach o długości 2 i 8 wiedząc, że w ten trapez wpisano okrąg.
23 paź 19:24
kochanus_niepospolitus:
zastosuj dwa wzory:
a+b = c+d (suma boków na przeciw siebie jest sobie równa)
Czyli: Obw = 2(a+b) = 2*(2+8) = ...
oraz:
wyznacz P
PS. Znajomość twierdzeń się kłania. Tutaj ściągawka:
https://matematykaszkolna.pl/strona/874.html
23 paź 19:32
kochanus_niepospolitus:
Oczywiście ... z drugiego równania (po zastosowaniu wzoru na pole trapezu) wyliczysz najpierw
promień okręgu, ale to już później pozwoli Ci na obliczenie samego pola (jaka jest zależność
pomiędzy wysokością trapezu h, a promieniem okręgu wpisanego w tenże trapez

)
23 paź 19:34
Krzysztof99: Dobra oba te twierdzenia znam, ale wyznaczając P dostaję P=10r (albo (r*obw)/2 ) no ale
wstawiając to do drugiego równania (po skorzystaniu ze wzoru na pole) dostaję 2r=h , czyli
nic. Albo po prostu jestem głupi i tyle. Jakąś lepszą wskazówkę lub całe bym prosił

23 paź 20:00
kochanus_niepospolitus:
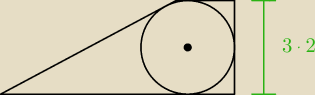
Przemyślałem trochę to co napisałem i faktycznie ... to za mało aby obliczyć pole.
Przy obecnych danych NIE DA się obliczyć pola trapezu (może to jest jakiś konkretny trapez, np.
równoramienny albo prostokątny?)
23 paź 20:14
kochanus_niepospolitus:
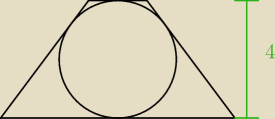
23 paź 20:18
Krzysztof99: http://pl.spoj.com/problems/FR_03_15/ to jest link do zadania, tam nie ważne co piszą w aspekcie programowania, bo tak czy
inaczej to pole musi być policzone. Też jakoś mi się wydaje że za mało danych albo źle
interpretuję, ale nie wiem, proszę o pomoc

23 paź 20:18
Krzysztof99: ++
23 paź 20:26
kochanus_niepospolitus:
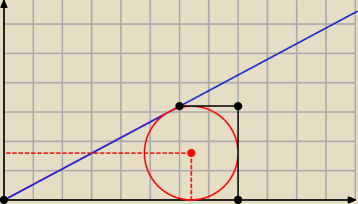 (x− 6.4)2 + (y− 1.6)2 = 1.62
(x− 6.4)2 + (y− 1.6)2 = 1.62
z konstrukcji i położenia okręgu od razu widać, że okrąg ten ma jeden punkt wspólny z
odcinkami:
A = {(0,0) , (8,0)}
B = {(8,0) , (8, 3.2)}
C = {(6, 3.2) , (8, 3.2)}
Sprawdzimy, czy ów
okrąg i
prosta mają dokładnie jeden punkt wspólny:
| | 32 | | 8x | | 8 | | 8 | |
(x− |
| )2 + ( |
| − |
| )2 = ( |
| )2 //* 152 |
| | 5 | | 15 | | 5 | | 5 | |
(15x − 96)
2 + (8x − 24)
2 = 24
2
225x
2 − 2880x + 9216 + 64x
2 − 384x + 576 = 576
289x
2 − 3264x + 9216 = 0
Δ = 10653696 − 4*289*9216 =
0
Czyli jest dokładnie JEDNO rozwiązanie tego układu.
A więc ten okrąg jest wpisany w trapez o punktach:
(0,0) , (8,0) , (8, 3.6), (6, 3.6)
pole tego trapezu będzie wynosić 18 [j
2].
23 paź 20:45
kochanus_niepospolitus:
Tak więc, pole trapezu uzależnione jest od dodatkowej informacji, której nie mamy podanej.
23 paź 20:47
Krzysztof99: Czyli czekaj, na danych z treści się nie da? Bo sie pogubiłem, to jeśli się nie da, to skąd to
18 na końcu (w przykładzie jest 20). W sensie dałeś jakieś dodatkowe założenie, czy coś
przyjąłeś w tym rozwiązaniu i jeszcze skąd y=8/15x

Totalnie nie ogarniam

23 paź 20:55
kochanus_niepospolitus:
Krzysztof 99
o 20:14 i 20:18 naszkicowałem Ci dwa trapezy:
1) jest to trapez prostokątny
2) jest to trapez równoramienny
w oba te trapezy udało mi się wpisać okrąg (o 20:45 udowodniłem, że w tenże prostokątny trapez
ten okrąg faktycznie jest wpisany).
Tak więc, mamy dwa różne trapezy spełniające wymagania zadania, które jednocześnie posiadają
RÓŻNE

pola.
23 paź 20:58
kochanus_niepospolitus:
y = 8x/15 to prosta przechodząca przez dwa wierzchołki trapezu (0,0) i (6, 3.2)
PS. o 20:45 błąd na końcu ... współrzędne tych punktów to oczywiście:
(0,0) , (8,0) , (8, 3.2), (6, 3.2)
23 paź 21:00
Krzysztof99: Aa, okej dobra łapię, to bubel jakiś i tyle, dziękuję bardzo

23 paź 21:15
Mila:
Wygląda na to, że Jasiu, poprawił rysunek. Narysował trapez równoramienny i otrzymał pole
P=20
To chyba policzysz, czy rysować i liczyć?
23 paź 21:43
Krzysztof99: Nie no tak, to dam radę

dzięki
23 paź 21:49
Eta:
Za mało danych ( przy dowolnym trapezie różnoramiennym
Dla trapezu równoramiennego : długości ramion c=5 to h=2r=4
pole P= 20
24 paź 18:39
Mila:
Dziękuję, tak myślałam

24 paź 18:40
kochanus_niepospolitus:
Miluś ... toć ja to napisałem wcześniej ... Ty mi nie wierzysz


24 paź 18:41
Eta:
"kochanusku"
Facetom nie raz..........się nie wierzy

24 paź 18:44
Mila:
Arturku, jestem trochę leniwa i nie czytałam wszystkich komentarzy

24 paź 18:48
24 paź 18:49
5-latek: Zarazem
Dobry wieczor 
24 paź 18:50
Mila:
Dobry wieczór

24 paź 19:15
 )
)

 Przemyślałem trochę to co napisałem i faktycznie ... to za mało aby obliczyć pole.
Przy obecnych danych NIE DA się obliczyć pola trapezu (może to jest jakiś konkretny trapez, np.
równoramienny albo prostokątny?)
Przemyślałem trochę to co napisałem i faktycznie ... to za mało aby obliczyć pole.
Przy obecnych danych NIE DA się obliczyć pola trapezu (może to jest jakiś konkretny trapez, np.
równoramienny albo prostokątny?)



 Totalnie nie ogarniam
Totalnie nie ogarniam
 pola.
pola.

 dzięki
dzięki






