Współrzędne na podstawie wektorów Cyder: Hej W kwadracie ABCD znane są współrzędne przeciwległych wierzchołków A(−2,2), C(4,0). Znajdź B i D Nie wiem jak wektor napisać więc zastosowałem ułamek...

	= [6,−2]
AC

S − środek między pkt A i C oraz pkt przecięcia przekątnych w kwadracie

	= [3,−1]
AS

S(1,1)

	⊥
SB		AS

Generalnie z rysunku i z tego przykładu wiem jak to zrobić na czuja, ale nie wiem zbytnio jak mogę z tego wyznaczyć pkt B i D nie posługując się rysunkiem a wzorami Musi być to oparte na wektory, innymi sposobami też umiem.

gospodarz: Wyznacz S środek przekątnej, potem równania: prostej BD (prostopadła do AC) i okręgu o środku S i promieniu AS

Ariel: To nie bedzie oparte na wektorach

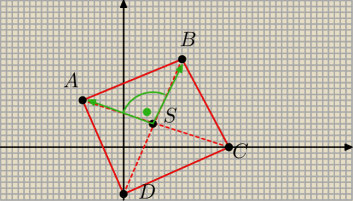3Silnia&6: AS ⊥ BS → AS = [3, −1] ⇒ BS = [−1, −3] → B=(2,4) AS ⊥ DS → AS = [3, −1] ⇒ DS = [1, −3] → B=(0,−2) A skad sie wziely wektory BS i DS ? Skoro maja byc prostopadle do wektora AS = [3, −1] to musza byc postaci [−1, −3], [1, −3] − trzeba zamienic miejscami i dodac minus w jednej wspolrzednej, jak przy prostych, gdzie iloczyn wspolczynnikow kierunkowych musial byc rowny −1 A skad wiedziec ktory to BS, a ktory to DS − z rysunku, ale mozna tez nie rysowac i przyjac jak chcesz, czy przyjme wierzcholek B u gory czy na dole to bez roznicy Mala poprawka, wektorem prostopadym do wektora [x.y] jest tez wektor [−ay, ax], gdzie a∊R np [1,2] ⊥ [−20,10], ale my za "a" przyjmujemy 1, bo wektory musza miec rowną długość (wszystkie trzy wektory AS, BS i DS maja dlugosc polowy przekatnej kwadratu )

Ariel: https://matematykaszkolna.pl/forum/306430.html

Cyder: Ok dzięki.