 3x−y+2=0 to y=3x+2 (rozowa
To jest moja taka propozycja
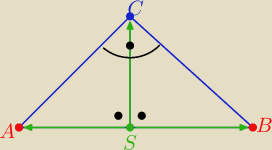
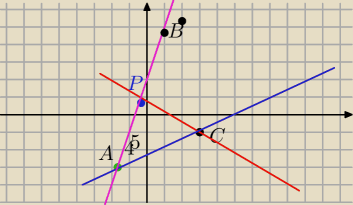
Nie jest to dokładny rysunek bo nie chce mi się liczyc dokładnie ale szkic
1) wyznaczyl równanie prostej prostopadlej do y=3x+2 i przchoczacej przez punkt C
2) wyznaczyl punkt przecięcia obu prostych P (będzie to srodek odcinka AB(przeciwprostokątnej
3. Wyznaczyl równanie prostej przecinajaca prosta y=3x+2 pod katem 45 stopni i
przecchpodzacej przez punkt C
4. Wyznaczyl wspolrzedne punktu A ( na rysunku widać które proste wziąć do obliczenia
5) Wspolrzedne punktu B z e wzoru na srodek odcinka
3x−y+2=0 to y=3x+2 (rozowa
To jest moja taka propozycja
Nie jest to dokładny rysunek bo nie chce mi się liczyc dokładnie ale szkic
1) wyznaczyl równanie prostej prostopadlej do y=3x+2 i przchoczacej przez punkt C
2) wyznaczyl punkt przecięcia obu prostych P (będzie to srodek odcinka AB(przeciwprostokątnej
3. Wyznaczyl równanie prostej przecinajaca prosta y=3x+2 pod katem 45 stopni i
przecchpodzacej przez punkt C
4. Wyznaczyl wspolrzedne punktu A ( na rysunku widać które proste wziąć do obliczenia
5) Wspolrzedne punktu B z e wzoru na srodek odcinka
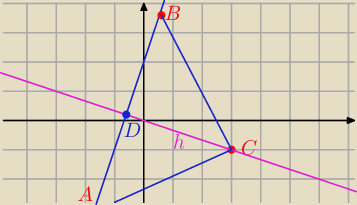 C = ( 3; − 1)
y = 3 x + 2
C = ( 3; − 1)
y = 3 x + 2
| 1 | ||
y = − | x + b | |
| 3 |
| 1 | ||
− 1 = − | *3 + b | |
| 3 |
| 1 | ||
y = − | x | |
| 3 |
| 1 | ||
3 x + 2 = − | x / * 3 | |
| 3 |
| 3 | ||
x = − | ||
| 5 |
| 3 | 9 | 10 | 1 | |||||
y = 3*( − | ) + 2 = − | + | = | |||||
| 5 | 5 | 5 | 5 |
| 3 | 1 | |||
D = ( − | ; | ) | ||
| 5 | 5 |
| 3 | 1 | 18 | 6 | |||||
h2 = I CD I2 = ( 3 + | )2 + ( − 1 − | )2 = ( | )2 + ( − | )2 = | ||||
| 5 | 5 | 5 | 5 |
| 324 | 36 | |||
+ | = | |||
| 25 | 25 |
| 360 | ||
= | ||
| 25 |
| 3 | 1 | 360 | ||||
( − | − x)2 + ( | − 3x − 2)2 = | ||||
| 5 | 5 | 25 |
| 9 | 6 | 9 | 54 | 360 | |||||
+ | x + x2 + ( − | )2 + | x + 9 x2 = | ||||||
| 25 | 5 | 5 | 5 | 25 |
| 9 | 81 | 360 | ||||
10 x2 + 12 x + | + | = | / * 25 | |||
| 25 | 25 | 25 |
| − 30 − 60 | 9 | − 30 + 60 | 3 | |||||
x = | = − | lub x = | = | |||||
| 50 | 5 | 50 | 5 |
| −9 | 27 | 10 | 17 | 3 | 10 | |||||||
y = 3* | + 2 = − | + | = − | lub y = 3* | + | = | ||||||
| 5 | 5 | 5 | 5 | 5 | 5 |
| 19 | ||
| 5 |
| 9 | 17 | 3 | 19 | |||||
A = ( − | ; − | ) B = ( | ; | ) | ||||
| 5 | 5 | 5 | 5 |

 bo I ∡ ACD I = 45o
bo I ∡ ACD I = 45o

| 1 | ||
Prosta CD : y = − | x | |
| 3 |
 S −− środek AB
C(3,−1) AB: y= 3x+2 to CS⊥AB ma równanie
S −− środek AB
C(3,−1) AB: y= 3x+2 to CS⊥AB ma równanie
| 1 | 1 | |||
CS: y= − | (x−3)−1 ⇒ CS: y= − | x | ||
| 3 | 3 |
| 1 | 3 | 1 | ||||
CS∩AB={S} 3x+2=− | x ⇒ 9x+6=−x ⇒ x=− | to y= | ||||
| 3 | 5 | 5 |
| 18 | 6 | |||
→ SC=[ | , − | ] to z warunku prostopadłości: | ||
| 5 | 5 |
| 6 | 18 | 6 | 18 | |||||
→SA=[ | , | ] lub [ − | , − | ] | ||||
| 5 | 5 | 5 | 5 |
| 3 | 6 | 1 | 18 | |||||
zatem xA+ | = | i yA− | = | |||||
| 5 | 5 | 5 | 5 |
| 3 | 19 | 3 | 19 | |||||
xA= | i yA= | to A( | , | ) | ||||
| 5 | 5 | 5 | 5 |
| 3 | 6 | 1 | 18 | |||||
oraz xB+ | =− | i yB− | =− | |||||
| 5 | 5 | 5 | 5 |
| 9 | 17 | 9 | 17 | |||||
xB=− | i yB= − | to B(− | , − | ) | ||||
| 5 | 5 | 5 | 5 |