 Mógłby mi ktoś wytłumaczyć czemu po rozłożeniu sumy na części mamy − 1 na samym końcu?
Naprawdę tego nie rozumiem.
n
∑ 2k = 2n+1 − 1
k=0
Mógłby mi ktoś wytłumaczyć czemu po rozłożeniu sumy na części mamy − 1 na samym końcu?
Naprawdę tego nie rozumiem.
n
∑ 2k = 2n+1 − 1
k=0
| 1−2n+1 | 1−2n+1 | |||
suma = 20+21+...+2n = 1* | = | =2n+1−1 | ||
| 1−2 | −1 |
| 1 − qn+1 | 1 − 2n+1 | |||
Sn+1 = a1* | = 1* | = 2n+1 − 1 | ||
| 1 − q | 1 − 2 |
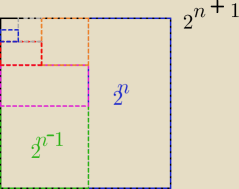 ale to też mógłbyś patrzeć w ten sposób jak na rysunku
Jak widzisz .. 2n zajmuje połowę przestrzeni 2n+1,
z tego co zostało (czyli 2n) połowę zajmuje 2n−1
z tego co zostało (czyli 2n−1) połowę zajmuje 2n−2
itd. itd. aż w końcu zostanie przestrzeń równa 2 ... której połowę zajmie 20 = 1 ... a więc
zostanie nie zajęta przestrzeń = "1".
ale to też mógłbyś patrzeć w ten sposób jak na rysunku
Jak widzisz .. 2n zajmuje połowę przestrzeni 2n+1,
z tego co zostało (czyli 2n) połowę zajmuje 2n−1
z tego co zostało (czyli 2n−1) połowę zajmuje 2n−2
itd. itd. aż w końcu zostanie przestrzeń równa 2 ... której połowę zajmie 20 = 1 ... a więc
zostanie nie zajęta przestrzeń = "1".
| 1 | ||
chociaż to rozumowanie bardziej się przydaje przy ∑ | ||
| 2n |
