Funkcje trygonometryczne - podstawowe pytanko Ania: Hej, mam problem z trygonometrią, samo obliczanie sinusów itp nawet ogarniam, jednak problem pojawia się w zadaniu, gdy trzeba rozwiązać nierówność. Powiedzmy a) 2sinx < √2 Rozwiązałam to w taki sposób: 2sinx < √2 /:2 sinx < √2/2 sinx = sin ^π₄, gdy x = sin^π₄ + 2Kπ lub x=sin ^π₄ − 2Kπ − Prosiła bym o sprawdzenie tego, Jednak wiem też, że to nie koniec i trzeba teraz narysować wykres a tu, że tak powiem wszystko leży. Prosiła bym ogromnie o wytłumaczenie jak i co narysować/zaznaczyć. [FSerdecznie dziękuję i pozdrawiam]]

Eta: https://matematykaszkolna.pl/strona/1578.html

Ania: Dzięki za link, jednak dalej nie do końca rozumiem co powinnam zrobić z tym wykresem.

Mila:

	√2
sinx=
	2

	π		π		3π
x1=		+2kπ lub x2=π−		+2kπ=		+2kπ
	4		4		4

	√2
sinx<
	2

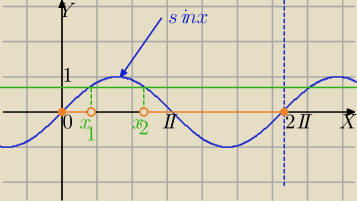
	√2
wykres sinusa leży poniżej prostej y=
	2

	π		3π
dla x∊<0+2kπ,		+2kπ) ∪(		+2kπ,2π+2kπ>
	4		4

'Leszek: Mozna to zapisac przy uzyciu jednego przedzialu otwartego bo sin x < √2/2 x ε ( 3π/4 + 2kπ ; 9π/4 + 2kπ )

Ania: Czuję, że będzie ciężko. Rysuję wykres, następnie w tym wypadku sinusoidę i nie mam pojęcia, co dalej, jak ją przekształcić?

Jerzy: A po co masz ją przekształcać i w co ?

Mila: Aniu, odczytujesz dla jakich argumentów wykres sinusoidy

	√2
leży poniżej wykresu prostej y=		.
	2

Masz na osi zaznaczone te argumenty kolorem pomarańczowym. Można to zrobić w przedziale <0,2π> albo tak , jak napisał Leszek .

Ania: Właśnie znalazłam dobry poradnik, dziękuję za wytłumaczenie i cierpliwość Za chwilkę zrobię jakiś przykładzik i wrzucę tutaj dla sprawdzenia.

Ania: 2sinx ≥ √3 sinx ≥ √3/2 sinx ≥ π/3 *Na wykresie zaznaczyłam argumenty: π/3 i 2π/3, a przedział mam taki: xε <π/3+2Kπ, 2π/3+2kπ>*

Jerzy:

Jerzy: Tam usuń ostatni wiersz: sinx ≥ π/3 ( to jest bez sensu)

Ania: Poprosiłabym jeszcze o wyjaśnienie takich nierówności: a) sin²x < 1 b) cos²x >1/2 Z góry dziękuję

kochanus_niepospolitus: sin²x < 1 ⇔ dla każdego x poza takim kiedy sin²x =1 ... czyli kiedy sinx=−1 lub sinx = 1