TRYGONOMETRIA Klaudia33: Rozwiaz nierownosci 1. 2cos²x +cos x <1 2cos²x + cos x −1 < 0 Podstawaim parametr t = cosx 2t² + 2 − 1 <0 Δ=9

	1
miejsca zerowe wyszły mi −1 oraz		i z tego wychodzi mi przedział od −1 do 1/2
	2

podstawiam to pod cosinus i juz mam inne wyniki, czy ktos widzi błąd? Z gory dzieki za pomoc <3

Adamm: nie ma błędu w tym co napisałaś pewnie nie potrafisz rozwiązać nierówności −1<cosx<1/2

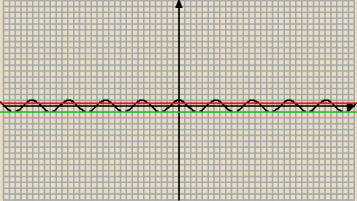
asdasd: −1 < cosx < 1/2 x∊(−π + 2kπ; −π/3 + 2kπ) u (π/3 + 2kπ; π + 2kπ), gdzie k ∊C Nie wiem czy poprawnie

Milo: Δ = 2² + 4*2 ≠ 4 + 8 = 12

Milo: ** Powinno być = zamiast ≠

asdasd: Delta chyba 9, tylko po podstawieniu t jakaś inna ta lewa strona w pytaniu, bo raczej: 2t² + t − 1 > 0, delta = 9

Milo: Racja, myślałem, że tam są 2t :x

Adamm: Milo Δ=1²+4*1

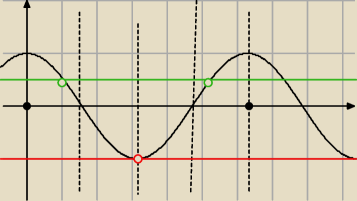
5-latek: Przepraszam ze sie wlacze do tego tematu na przedziale [0 ,2π] −1<cosx<0,5

	5π
x∊(π/3,		)
	3

czyli ogolne rozwiazanie to x∊(π/3. 5π/3)+2kπ Teraz mam problem tez czy wylaczyc z rozwiazania w tym przedziale π cosπ=−1 jesli podsatwimy cosπ do rownania wyjsciowego bedziemy mieli 2*(−1)²−1−1<0 czyli 0<0 czy ta nierownosc dla cosπ jest spelniona ?

Adamm: pytasz się czy 0<0 ? 0 nie jest mniejsze od 0 0 jest równe 0

5-latek: Dobry wieczor . Tak. Oto pytalem czyli nierownosc wyjsciowa jest niespelniona dla cosπ wiec z rozwiazania nalezy wylaczyc π czyli ogolne bedzie x∊(π/3, 5π/3)\π+2kπ czy jest dobrze ?

Adamm: x∊(π/3; π)∪(π; 5π/3) ogólne rozwiązanie to x∊(π/3+2kπ; π+2kπ)∪(π+2kπ; 5π/3+2kπ) gdzie k∊C

Adamm: a jak byś zapisał to porządnie? (o ile rozumiem o co chodzi, to zapis jest tragiczny)

5-latek: I oto chodzilo dziekuje Ci

Adamm: chcę po prostu się upewnić że (bo podobno chciałeś poprawiać maturę) nie napiszesz na niej czegoś takiego

5-latek: czyli lepiej pisac w przedzialach +2kπ czy +kπ

Adamm: nie rozumiem o co pytasz

5-latek: Adamm Napisalem rozwiazania drugiej nierownosci Zobacz jesli mozesz czy tak ma byc . jesli tak to oto wlasnie pytalem

5-latek: https://matematykaszkolna.pl/forum/357362.html Tutaj