eee
imie: Funkcja liniowa określona jest wzorem f(x)= −
√3x +6. Funkcja ta przyjmuje wartości dodatnie
tylko wtedy gdy?
wynik 2
√3
i która odp i dlaczego
chodzi o te dodatnie wartości
to ujemne będa miały przeciwny znak
x>2
√3
x<2
√3
13 sie 17:46
Jerzy:
Gdy −√3x + 6 > 0 i wyznacz x
13 sie 17:53
Jolanta: masz jakies pytania ?
13 sie 18:51
imie: cały czas to samo bo Jerzy nic nie wyjaśnił
rozwiązałem ten X i mówie ze to 2 pierw 3
ale w odpowiedziach są ujemne to wykluczyłem i zostały odpowiedzi z < > a tutaj nie wiem które
wybrać
13 sie 18:58
Jerzy:
| | 6 | |
x > |
| i usuń niewymierność mianownika. |
| | √3 | |
13 sie 19:03
imie: 2 pierw 3
13 sie 19:06
Jerzy:
| | 6 | |
Kużwa... odwrotnie znak x < |
| |
| | √3 | |
13 sie 19:07
bosa_Lu:
−√3 x +6>0⇔
−√3x>−6 /*(−1)
√3x<6 /*√3
3x<6√3 /:3
x<2√3
13 sie 19:07
imie: no tak −1 zmienia znak a na początku to skąd mam wiedziec który dać zeby potem dobrze zmienic?
13 sie 19:12
Jerzy:
Dzielisz przez liczbę ujemną,więc zmieniasz znak.
13 sie 19:20
Mila:
Na początku przepisujesz wzór funkcji i piszesz znak :
f(x)> 0 to oznacza że badasz dla jakich x−ów wartości funkcje są dodatnie ( większe od
zera)
Jeśli chcesz wiedzieć dla jakich x−ów wartości funkcji są ujemne piszesz :
f(x)<0 (wartości funkcji mniejsze od zera)
13 sie 19:22
Jerzy:
Witaj
Mila 
pozdrawiam
13 sie 19:41
Mila:
Witam ciepło
13 sie 19:54
Jolanta: imie porozmawiamy sobie o funkcji liniowej ?
13 sie 20:48
5-latek: Myslisz ze go /ja to interesuje ?
13 sie 21:11
Mila:
Witaj
5−latku: Zadowolony po podróży?
13 sie 21:15
imie: mozemy
dzięki Mila za odp takiej oczekiwałem
13 sie 21:42
5-latek: Dobry wieczor
Milu
tak jestem zadowolony i to bardzo chociaz z powodu urlopu ziecia musielismy zjechac
wczesniej do domu
Ale i tak bylem ponad tydzien u nich .Zwiedzielem duzo , schudlem 3 kilo nawet
Kiedy wybierasz sie na urlop?
13 sie 21:49
Jolanta: funkcja liniowa dana jest wzorem y=ax+b − jest to równanie kierunkowe prostej
co powiesz o monotonicznosci ?
13 sie 21:53
imie: no stwierdza to czy jest rosnąca czy malejąca czy stała
13 sie 21:59
Jolanta: kiedy stała?
13 sie 22:02
Jolanta: wiesz ?
13 sie 22:06
imie: chyba jak a jest równe zero
albo jak jakieś tam iksy są takie same
13 sie 22:06
5-latek: Zonk
np x=5 to nie jest funkcja
13 sie 22:08
Jolanta: tak jeżeli a (czyli wspólczynnik kierunkowy) =0
np y=5 y=−2
(0*x=0 czyli zostaje samo b)
co jest wykresem y=2 ?
13 sie 22:09
imie: nofunkcja stała w 2 na pionowej kresce
13 sie 22:12
Jolanta:
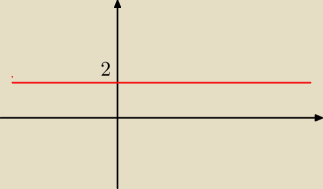
prosta równoległa do osix
okresl monotonicznosć
y=−
√3x+4
13 sie 22:15
Jolanta: nad czym myślisz?
13 sie 22:18
Jolanta: wiesz ? odpowiadaj jak najszybciej bo szkoda czasu
13 sie 22:21
imie: nie wiem
13 sie 22:23
imie: nawet wolfram nie pomógł
13 sie 22:25
Jolanta: y=ax+b
a=0 stała
a>0 rosnąca
a<0 malejąca
y=−√3x+4 a<0 czyli funkcja malejąca
13 sie 22:25
Jolanta: umiesz narysować wykres prostej y=2x+1 ?
13 sie 22:27
imie: no ale zrobic to na rysunku to juz nie wiem jak
13 sie 22:27
Jolanta: na kartce narysujesz ?
13 sie 22:28
imie: no rosnąca przechodzi przez 1 na pionowej
13 sie 22:29
Jolanta: a dla jakch argumentów (czyli x) przyjmuje wartści dodatnie (czyli y>0)
13 sie 22:31
Jolanta: w którym miejscu przecina os x ?
13 sie 22:34
Jolanta: wiesz ?
13 sie 22:35
imie: −1/2 ?
13 sie 22:36
Jolanta: narysowałes na kartce w kratkę ?
13 sie 22:37
Jolanta: | | −1 | |
tak x= |
| to miejsce......... dokończ |
| | 2 | |
13 sie 22:38
imie: nom na zwyklej
13 sie 22:38
Jolanta: to miejsce zerowe
13 sie 22:40
imie: zerowe
13 sie 22:41
imie: tak
13 sie 22:41
Jolanta: jeżeli masz funkcję liniową to z jednej strony miejsca zerowego funkcja przyjmuje wartości
dodatnie a zdrugiej ujemne ,tak ?
13 sie 22:42
imie: tak
13 sie 22:43
Jolanta:
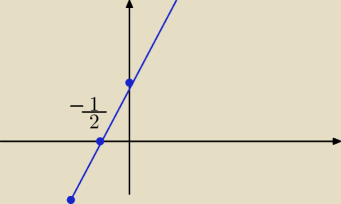
y=2x+1
y<0 2x+1<0
2x<−1
13 sie 22:50
Jolanta: | | 1 | |
dla x∊(−∞,− |
| ) funkcja przyjmuje wartości ujemne |
| | 2 | |
jasne ?
13 sie 22:51
imie: nom
13 sie 22:53
Jolanta: dla jakich argumentów funkcja przyjmuje wartosci dodatnie?
13 sie 22:54
Jolanta: czego nie rozumiesz ?
13 sie 22:54
imie: −1/2∞
13 sie 22:56
imie: mozesz spojrzec na inne moje zadanie
13 sie 22:56
13 sie 22:57
Jolanta: daj
13 sie 22:57
imie: 2x2−5x−3≤0
no i wynik to (−3, 1/2)
co za besens
przeciez mam znak ≤ zamiast < to czemu nawiasy nie sa ostre
i a jest dodatnie wiec parabola w górę czyli plusy są po bokach czyli powinno byc
(− ∞; −3> u <1/2; +∞ )
13 sie 23:01
imie: 5 jest dodatnia przy iksie
13 sie 23:01
Jolanta: policzΔ
13 sie 23:02
imie: a dobra, te znaki chyba znacza ze wartosci sa ujemne
ale i tak bym dał w odpowiedzi ostre nawiasy
13 sie 23:03
imie: juz policzyłem, wynik ok
delta 49 = 7
13 sie 23:03
Jolanta: jeżeli masz taki wynik tzn ze powinno byc <0 a nie ≤0
13 sie 23:04
Jolanta: policz x1 i x2
13 sie 23:06
imie: to moze błąd bo zadania napisane przez kogoś dla mnie
−5−7 / 4 = −3
−5+7 /4 = 1/2
13 sie 23:08
Jolanta: | | −b−√Δ | | −5−7 | | −12 | |
wzór x1= |
| = |
| = |
| =−3 |
| | 2a | | 4 | | 4 | |
13 sie 23:09
Jolanta: dobrze teraz robisz wykres
| | 1 | |
na osi zaznaczasz −3 i |
| i rysujesz parabole z ramionami do góry,tak na oko |
| | 2 | |
13 sie 23:11
imie:
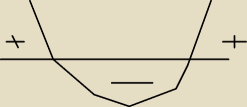
no i w prawo nawias
to są ujemne
13 sie 23:13
Jolanta:
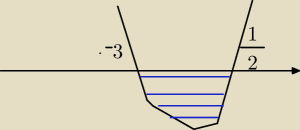
13 sie 23:14
Jolanta: 2x2+5x−3<0 czyli y<0
13 sie 23:15
Adamm: tam jest 2x2+5x−3 czy 2x2−5x−3 w końcu
13 sie 23:17
imie: 5x dodatnia
13 sie 23:18
Jolanta: | | 1 | |
y=2x2+5x−3 y=0 2x2+5x−3=0 dla x=−3 x= |
| |
| | 2 | |
| | 1 | |
y>0 2x2+5x−3>0 dla x ∊(−∞−3)v( |
| ,∞) |
| | 2 | |
y<0 dokończ
13 sie 23:18
13 sie 23:20
Jolanta: | | 1 | |
jeżeli masz 2x2+5x−3≤0 to odpowiedz x∊<−3. |
| > |
| | 2 | |
13 sie 23:25
Jolanta: wiesz dlaczego ?
13 sie 23:26
imie: nom
13 sie 23:26
imie: tak
13 sie 23:26
imie: bo mniejsze lub równe
13 sie 23:27
Jolanta: dobrze masz jeszcze jakies zadanie?
13 sie 23:27
imie: przekątne rombu mają długości 6 i 8
wyznacz h
13 sie 23:29
Jolanta: myślalam o paraboli.łWaściwie dlaczego robisz zadania
13 sie 23:32
13 sie 23:32
imie: do matury
13 sie 23:33
13 sie 23:34
imie: thx
13 sie 23:35
Jolanta: Radziłabym skupic sie na jednym temacie.Moze jeszcze pociągniemy funkcje?
13 sie 23:36
imie: największa wartosc funkcji kwadratowej jest rowna 9
liczby 0 i 6 sa miejscami zerowymi tej funkcji
a)zapisz wzor funkcji f w postaci ogolnej
b) dla jakich x wykres funkcji f lezy powyzej wykresu funkcji okreslonej wzorem y=x+4?
13 sie 23:41
Jolanta: a=5 z tw Pitagorasa a=
√32+42
P=24
13 sie 23:42
Jolanta: jaka wiadomość wynika z tego ,ze najwieksza wartość wynosi 9?
13 sie 23:43
Jolanta: jak parabola ma ramiona?
13 sie 23:45
Eta:
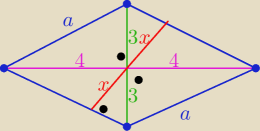
a=
√42+32=5
| | 4*3 | | 12 | | 24 | |
x= |
| = |
| h=2x= |
| |
| | 5 | | 5 | | 5 | |
13 sie 23:46
Jolanta: narysuj 2 parabole ,jedna z ramionami w dól,druga w górę
co powiesz na temat wartości ,które przyjmują
13 sie 23:49
Jolanta: jeżeli parabola ma ramiona w dól,to gdzie jest najwiekszy y?
13 sie 23:50
imie: ale to do punktu a
ja bym tylko podstawił miejsca zerowe do wzoru do iloczynowej a z potem do ogolnej
13 sie 23:52
imie: −6?
13 sie 23:53
imie: 6
13 sie 23:54
Jolanta:
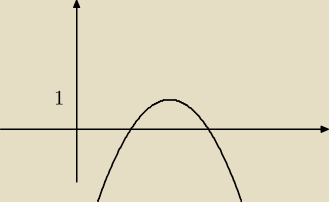
np taka parabola
13 sie 23:54
parabola:
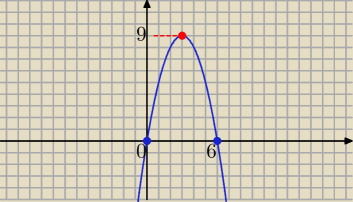
13 sie 23:56
imie: no a ten wierzchołek to skąd
z wzoru na p i q
13 sie 23:57
imie: ale do tego potrzebuje pierw w ogolnej postaci
13 sie 23:58
Adamm: fakt: wierzchołek leży zawsze między miejscami zerowymi, jeśli istnieją
13 sie 23:58
Jolanta: jezeli istnieje wartosć najwieksza to znaczy ,że parabola ma ramiona w dół i mamy dany
wierzchołek
dla x
w y=9
13 sie 23:59
imie: ok czaje
14 sie 00:00
imie: mam tutaj a ?czy to bedzie 1
14 sie 00:05
Jolanta: f(x)=a(x−p)2+q
f(x)=a(x−3)2+9
f(0)=
14 sie 00:06
imie: x
2−6x+18
14 sie 00:07
Jolanta: wykorzystuje miejsce zerowe x=0 y=0
a(−3)2+9=0
14 sie 00:07
Jolanta: nie możesz mieć x2bo ramiona sa w dół
9a=−9
a=−1
14 sie 00:09
imie: tak, to −x ?
14 sie 00:10
imie: −9x2−6x+18?
14 sie 00:11
Jolanta: f(x)=−(x−3)2+9
f(x)=−x2+6x+18
14 sie 00:12
imie: powinno byc
y=−x2+6x
14 sie 00:15
imie: wg odpowiedzi
14 sie 00:15
Adamm: i tak jest
14 sie 00:15
Jolanta: tak
−x
2+6x−9+9
14 sie 00:16
Jolanta: teraz kiedy parabola ma większe wartosci od prostej
możesz sobie narysowac i sprawdzic
−x2+6x>x+4
14 sie 00:18
Jolanta: ile wyszła Δ?
14 sie 00:20
imie: mam x1 i x2 rozwiazac
14 sie 00:20
imie: 3
14 sie 00:21
imie: 4 i 1
14 sie 00:22
Jolanta: Δ=9 √Δ=3
tak x1 x2
14 sie 00:23
Jolanta: teraz wykres i odczytaj rozwiązanie
14 sie 00:23
imie: to musze tabelke robic tak?
14 sie 00:25
Jolanta: nie tabelkę robisz jeżeli ma być dokładny wykres
zaznaczasz na osi miejsca zerowe i na oko rysujesz ,,falbankę",wazne ,zeby miala ramiona
zgodnie z tym co pokazuje a
14 sie 00:27
Jolanta: f(x)=−x2+5x−4
a=−1 czyli ramiona...
14 sie 00:29
imie: ramiona w dół
14 sie 00:31
Jolanta: bylo tak
−x2+6x >x+4
−x2+5x−4>0
14 sie 00:32
Jolanta: x∊ ...
14 sie 00:33
imie: (1,4)
14 sie 00:34
Jolanta: tak
podsumujmy
jezeli masz −x2+5x−4=0 to liczysz Δ i miejsca zerowe x1 i x2
jezeli masz −x2+5x−4<0 (lub>0) liczysz jak wyzej a pózniej wykres i z niego odczytujesz
rozwiązanie nierówności
14 sie 00:38
imie: a jak delta ujemna to −b/2a?
14 sie 00:40
Jolanta: Po prawej stronie masz matury z rozwiązaniami,to dobry sposób na powtorkę
14 sie 00:40
imie: właśnie widziałem jak dodali posortowane tematycznie,chyba za to się wezmę
14 sie 00:43
Jolanta:
jezeli Δ<0 to parabola nie przecina osi x lezy nad osia jeżeli a>0 lub pod osia z ramionami w
dół gdy a<0
14 sie 00:43
Jolanta: to co napisałeś to wzór na obliczenie x
w.Korzystamy z niego niezaleznie od tego jaka jest Δ.z
| | x1+x2 | |
tym ,że jak masz dwa pierwiastki to możesz tak jak pisałam |
| |
| | 2 | |
14 sie 00:45
Jolanta: jak wejdziesz w matury to masz konkretne matury z ostatnich lat.Warto.Przekonasz sie,ze mozna
tresc zadania podac w rózny sposób.Musze isć spac,bo rano nie wstanę
14 sie 00:48
imie: ok, dzieki za wszystko
14 sie 00:54