... bringiton: odleglosc prostej 7=4−x od początku układu współrzędnych

Milo: Ta prosta na pewno tak wygląda? Jeśli tak to: 7=4−x x=4−7 x=−3 odległość od początku układu d=3

bringiton: przepraszam, y=4−x

Adamm: mając prostą postaci Ax+By+C=0 możemy obliczyć jej odległość od punktu (x₀; y₀) wzorem

	|Ax0+By0+C|
d=
	√A2+B2

mat: poczatek ukladu to (0,0) https://matematykaszkolna.pl/strona/1249.html

Jerzy: Wygrał mat

Adamm: Jerzy, to nie są zawody

bringiton: jakaś podpowiedź

mat: był(e)aś w ogóle na tej stronie? albo popatrzyl(e)as na to co napisal Adamm

bringiton: a po co

5-latek:

5-latek: Czyli ss s brington Kundelek , Sophie i jak jeszcze ?

bringiton: ej co sie podszywasz kolego Spojrzałem i nie wiem jak mam to y=4−x podstawic do wzoru

bringiton: btw, spojrzałem na sophie i ss, zdajesz sobie sprawe ze prawo do poprawki ma 15% maturzystow?

mat: y=4−x y+x−4=0 1*y+1*x+(−4)=0 A=1, B=1, C=−4

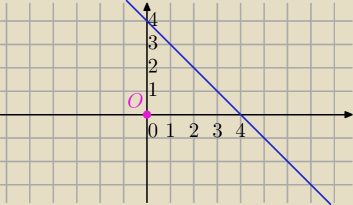
Mila: Dane jest równanie kierunkowe prostej: k: y=4−x Punkty wykresu (0,4), (1,3) O(0,0) Odległość punktu O od prostej: y=4−x przekształcamy na równanie w postaci ogólnej −x−y+4=0 /*(−1) k: x+y−4=0

	|1*x0+1*y0−4|
d(O,k)=		=
	√12+12

	1*0+1*0−4|		|−4|		4		4*√2
=		=		=		=		=
	√2		√2		√2		2

=2√2 ===

Mila: Bez tych wszystkich obliczeń. II sposób Zauważ, że masz tam Δ prostokątny równoramienny o przyprostokątnych równych 4. Odległość prostej od początku układu wsp. jest równa połowie przekątnej kwadratu o boku 4. p=4√2 d=2√2 Warto rysować proste w układzie wsp.