Nierownosc wymierna
5-latek: Rozwiaz nierownosc
| x2−(a+b)x+ab | |
| ≥0 |
| x2−(c+d)x+cd | |
gdzie a,b c d oznaczaja liczby R takie ze a<b<c<d
Zamieniam na postac iloczynowa
Moge wpisac do wolframa ale to nie o to chodzi
Po zamianie mam
x
4+(−a−b−c−d)x
3+(ab+ac+ad+bc+bd+cd)x
2+(−abc−abd−acd−bcd)x+abcd≥0
x
4−x
3(a+b+c+d) +x
2(ab+ac+ad+bc+bd+cd)−x(abc+abd+acd+bcd)+abcd≥0
dalej nie wiem co zrobic
czy wzory Vieta ? (tez nie wiem jak
A moze rozkladac osobno licznik i mianownik na czynniki ?
2 lip 12:42
luka: przeciez to łatwe
u góry masz np (a − x) (b − x)
2 lip 12:50
5-latek: Jak do tego doszsedles?
2 lip 12:53
Adamm: wzory Viete'a na przykład
2 lip 12:54
5-latek: Adamm czesc jak ?
2 lip 12:57
Adamm: iloczyn pierwiastków to ab, a suma a+b
jakie to mogą być pierwiastki?
no tylko a i b
2 lip 12:58
luka: x2−ax−bx+ab=a(b−x)−x(b−x)
to po prostu same dziłania
2 lip 12:58
Adamm: 5−latek cześć
2 lip 12:58
luka: tu nie trzeba znac wzrów vieta
2 lip 13:01
5-latek: Wzory Vieta dla trojmianu kwadratowego (osobno dla licznika i mianownika
a nie dla wielomianu stopnia czwartego tak ja sobie pomyslalem

2 lip 13:02
Adamm: dla wielomianu stopnia czwartego też możesz
od razu widać że pierwiastki to a, b, c, d
2 lip 13:03
luka: rozkład licznika i minownika na czynniki pierwsze wystarczy
2 lip 13:04
www: z jakiego poziomu to zadanie?
2 lip 13:05
5-latek: Ze zbioru zadan maturalnych
2 lip 13:06
Jack:
1) x
2 − x(a+b) + ab
Δ = (a+b)
2 − 4ab = (a−b)
2 ,no i teraz skoro a<b to a−b < 0
√Δ = |a−b| = b−a
2) x
2−x(c+d) + cd
analogicznie to samo
Δ = (c+d)
2 − 4cd
√Δ = |c−d| = d − c
x
2 = d
zatem tak naprawde wyglada to tak:
2 lip 13:07
5-latek: Witaj
Jack 
Wlasnie tak sobie teraz zrobilem
2 lip 13:09
Jack:
skoro a<b<c<d to odp. x ∊ (−∞;a> U <b;c> U <d;∞)
2 lip 13:10
Jack: witaj Krzysiu

2 lip 13:11
2 lip 13:11
5-latek:
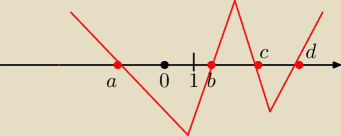
2 lip 13:14

 Wlasnie tak sobie teraz zrobilem
Wlasnie tak sobie teraz zrobilem

