Udowodnij ze jest to trójkąt rownoramienny Lola: . Okręgi k1 i k2 o środkach w punktach M i N mają jednakowe promienie i każdy z okręgów przechodzi przez środek dru− giego. Wierzchołki A i C trójkąta ABC leżą na k1, a punkt B na k2. Bok AB przechodzi przez N, a bok BC przez punkt S – punkt przecięcia obu okrę− gów. Pokaż, że trójkąt ABC jest rów− noramienny.

5-latek: https://matematykaszkolna.pl/forum/354604.html

Lola: To jest inne zadanie xd

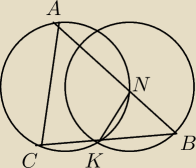
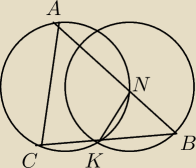jc: 1. ∡CBA = ∡KBN, ∡CAB = ∡CAN 2. |NK| = |BN| ⇒ ∡KBN = ∡BKN 3. ∡CKN = 180 − ∡BKN 4. ∡CKN = ∡CAN = 180 Z tego wszystkiego wynika, że ∡CBA =∡CAB, a więc |AC|=|BC|. (na rysunku wybrałem jedną z dwóch możliwości wyboru punktu C)