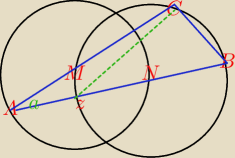
 Okręgi k1 i k2 o środkach w punktach M i N mają jednakowe promienie
i każdy z nich przechodzi przez środek drugiego.
Wierzchołki trójkąta ABC leżą na jednym lub na drugim okręgu, tak jak to pokazano na
rysunku obok. Punkt M leży na boku AC, a N na boku AB. Wyznacz miarę kąta C . Raz
przyjmij, że a = 18◦ , a następnie zrób to ogólnie przy dowolnym
kącie a.
wiem że zcb = 90 i to tyle proszę o pomoc
Okręgi k1 i k2 o środkach w punktach M i N mają jednakowe promienie
i każdy z nich przechodzi przez środek drugiego.
Wierzchołki trójkąta ABC leżą na jednym lub na drugim okręgu, tak jak to pokazano na
rysunku obok. Punkt M leży na boku AC, a N na boku AB. Wyznacz miarę kąta C . Raz
przyjmij, że a = 18◦ , a następnie zrób to ogólnie przy dowolnym
kącie a.
wiem że zcb = 90 i to tyle proszę o pomoc
| 180−3α | 3 | |||
|∡NCB| = |∡NBC| = | = 90 − | α | ||
| 2 | 2 |
| 3 | α | |||
|∡ACB| = |∡MCN| + |∡NCB| = 2α + 90 − | α = 90 + | |||
| 2 | 2 |
