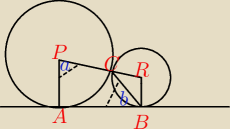
Zadanie 28, matura maj 2017 martazz: Dane są dwa okręgi o środkach w punktach P i R, styczne zewnętrznie w punkcie C. Prosta AB jest styczna do obu okręgów. odpowiednio w punktach A i B oraz |<APC| = α i |<ABC| = β (zobacz rysunek). Wykaż, że α = 180*−2β

martazz: Czy można poprowadzić prostą AC i na tej podstawie stwierdzić, że |<ACB| = 90* ? Czy coś totalnie pomyliłam?

Mila: Kilka razy jest to już wyjaśniane na forum. Musisz napisać dlaczego |<ACB| = 90.

Ana : <PAB i <RBA mają po 90 stopni. △RBC i △ACP są równoramienne, ponieważ ramionami są promienie kół. <BCR i <RBC oznaczmy sobie jako x. <CAP i <BAC oznaczamy jako γ <BAC oznaczamy jako p β+x=90* γ+p=90* γ+p=β+x <BAP+<ABR=2β+2x=180* => 2x=180*−2β <BRC=180*−2x 180*−2x=180*−α α=2x α=180*−2β cnu PS. Pamiętaj, ze miara wewnętrzna czworokąta wynosi 360*

martazz: Tak, wiem że kilka razy ale chodziło mi o ten konkretny przypadek, gdzie napisałam, że |<ACB| = 90*. Wie ktoś jak to porządnie wyjaśnić?

Mila: Tu masz wyjaśnione dlaczego ten kąt jest prosty. https://matematykaszkolna.pl/forum/353174.html