Wzory zef: Jakieś przydatne wzory których nie ma w kartach ? I podstawa i rozszerzenie.

Jack: błąd względny i bezwzględny... zawsz sie pojawia

Kacper: Na podstawie np. nierówność między średnimi do dowodu może się przydać. I jeszcze wzór na drogę

Eta: (n−2)*180^o = ............

n(n−3)
	= .....................
2

zef: Nierówności na podstawie ? Ale i bez tego da radę pewnie wybrnąć

Eta:

	2v1*v2
vśr=
	v1+v2

Jack: i w teorii, (chociaz watpie by bylo potrzebne) wzorek na prace, albo jak liczyc takie zadanie, ze jedna koparka jak kopie sama to 5h, druga jak sama to 10h i jak beda kopac razem to jak szybko skoncza? tego typu zadanka

Jack: a no bo podstawa...to tylko ten blad wzgledny i bezw.

zef: Eta co to za 2 pierwsze wzory ?

Eta: a_n=S_n−S_n−1 W ciągu arytm. S_n= m_e*n , m_e −−− mediana (środkowy wyraz) , n ilość wyrazów ciągu

Wac: Niuton hyba

Jack: na katy w dowolnym foremnym ile wynosi suma miar w 9−kacie? (9−2)*180 = ...

Eta: (n−2)*180^o−−− suma kątów wewnętrznych wielokąta wypukłego n −− ilość boków ( wierzchołków tego wielokąta

n(n−3)
	= ilość przekątnych wielokąta wypukłego
2

Wac: Kacper ale jaki wzur na drogę? chodzi Ci o sendymentacje asfaltu czy co S = L2 − L1 rozpisać Ci

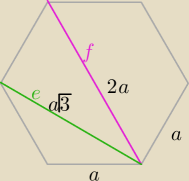
Eta: W sześciokącie foremnym o boku "a" f=2a −−− dł, dłuższej przekątnej e=a√3−−− dł. krótszej przekątnej R=a −− dł. promienia okręgu opisanego na sześciokącie foremnym

	a√3
r=		−− dł. promienia okręgu wpisanego w sześciokąt foremny
	2

zef: Coś jeszcze co może zaskoczyć ?

Wac: nw present simple powtórz ZAWSZE jes

Eta:

	p
Kk=Kp(1+		)n*k −− wzór na procent składany z kapitalizacją k razy w roku
	k*100

( bez podatku od odsetek) z podatkiem od odsetek np 20%

	p*0,8
Kk=Kp(1+		)n*k
	k*100

Eta: @Wac uspokój się! .........bo zaraz dostaniesz bana !

zef: Oki, też fajny wzorek którego nie ma Jak już jestem po polskim to z podstawą z matmy problemu chyba nie będę miał

Kacper:

	x1+x2
p=
	2

Eta: f(x)=ax²+bx+c

	x1+x2
xw=p=		i yw=q=f(p)
	2

W( x_w, y_w)

StrasznyNieogar: zef matemaks wrzucił chyba dziś albo wczoraj filmik z tymi wzorami Ale to chyba już wszystkie tu koledzy wymienili, które tam byly

Eta:

zef: Δ=b²−4ac

Eta:

Jack: byc moze, ze srodkowe w trojkacie przecnaja sie w stosunku 2:1 albo jakies inne wlasnosci dot. np. dwusiecznych, symetranych

zef: Nie mogę sobie przypomnieć jednej sprawy odnośnie tego że mamy jakiś trójkąta prowadzimy (najprawdopodobniej) wysokość i później jakiś odcinek jest średnią arytmetyczną tych 2 odcinków. Może wiecie o co mi chodzi ? Wykorzystuje się to w zadaniach na udowadnianie.

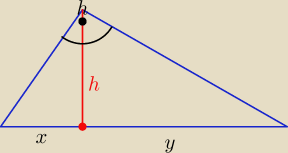
Eta: h²=x*y −−− średnia geometryczna

Omikron: Nie chodzi Ci o wysokość poprowadzoną z wierzchołka kąta prostego w trójkącie prostokątnym? Kwadrat jej długości jest równy iloczynowi odcinków na jakie dzieli przeciwprostokątną.

zef: Tak, to wiem ale chodzi mi o coś innego. Rozwiązanie zad 2 przez Bogdana. 272526 Z czego on tutaj skorzystał ?

zombi: Zawsze polecam https://pl.wikipedia.org/wiki/Twierdzenie_Stewarta na próbnych z 2 albo 3 razy mi się przydało, nie tak ciężko zapamiętać, a ułatwia czasami planimetrię

Kacper: Zef to zwykłe podobieństwo

Marcin: ja radze zapamietac własnosci miedzy srednimi np (x+y)/2>=√x*y

Kacper: Przydatne jeszcze twierdzenie o odcinku łączącym środki dwóch boków w trójkącie

Adam: Kacper, twierdzenie Talesa

Kacper: Twierdzenie Talesa jest w karcie wzorów ale to nie to samo. Poza tym na poziomie podstawowym nie ma tego twierdzenia w podstawie (co uważam za głupotę).