Test I Blue: Mógłby mi ktoś sprawdzić, czy to zadanie jest dobrze udowodnione?

	2
zad.11 Wykaż, że jeśli x>0, to x2 +		≥ 3.
	x

http://i60.tinypic.com/oeg5l.jpg I proszę o pomoc z tymi zadaniami (niestety planimetria) zad.1 Dany jest równoległobok ABCD oraz dowolne punkty E i F odpowiednio na bokach AB i CD. Uzasadnij, że pole czworokąta GEHF jest równe sumie pól trójkątów AGD i HBC. http://i61.tinypic.com/osh2zk.jpg zad.2 W trójkącie ABC punkty D, E leżą odpowiednio na bokach AB i AC tak, że |AD|: |DB|=1:2 oraz |AE|: |EC|=2:1. Udowodnij, że |EF|: |FB|=1:6 http://i61.tinypic.com/2rnkmso.jpg Proszę o pomoc

Eve: 11 ok

zombi: 11. Jest ok, ale standardowo można to przepchnąć ze średnich

2   x2+   x		1   1   x2 + +   x   x		1		1
	=		≥ 3√x2*		*		= 1
3		3		x		x

⇔

	2
x2+		≥ 3 koniec.
	x

Mila: 11) w Twoim sposobie zakończyłabym tak: x³−3x+2≥0⇔ (x−1)²*(x+2)≥0 nierówność spełniona dla x>0 ponieważ : (x−1)²≥0 dla każdego x∊R i x+2> 0 dla x>0. Reszta dobrze.

Blue: ok, Mila dzięki za uwagę

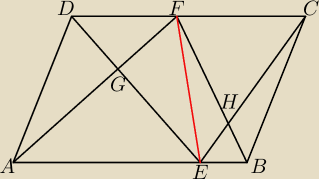
Bogdan: Podpowiedź do zadania 1. Wystarczy wykazać, że w w widocznych trapezach: AEFD i EBCF równe są pola trójkątów AGD i EGD oraz EHF i BHC

panpawel: do zad 2 chcesz jakieś hinty czy od razu całe rozwiązanie?

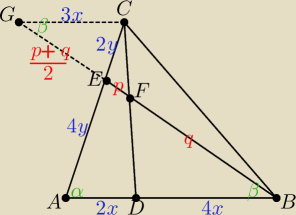
Bogdan: Wskazówka do zadania 2. Korzystamy z podobieństwa trójkątów: ABE i CGE oraz DBF i CGF.

Blue: Bogdan, pierwsze dokończyłam, potem zeskanuję i wrzucę, ale mógłbyś pokazać pełne rozwiązanie tego drugiego zadania Proszę

znawca: Drugie zadanie ciekawe

znawca: Ale wy go zrobić łatwo nie umiecie

Blue: Znawca, to może Ty je zrobisz?

Blue: Wrzucam skan tego 1 zadania: http://i60.tinypic.com/23a83r.jpg − czytajcie na odwrót − od prawej

Blue: Zrobi ktoś to 2? I powie, czy dobrze mam to 1

3Silnia&6: 2)lGFl / lFBl = lGCl / l DBl

p+q		3x
	+ p / q =
2		4x

2(3p + q ) = 3q 6p + 2q = 3q p/q = 1/6 swietne jest to rozwiazanie @Bogdana. nie wiem czy da sie latwiej, ale to jest na pewno bardzo oryginalne.

3Silnia&6: 1 tez przejdzie

Blue: Dzięki Silnia ! Przejdzie? Czyli mam nadzieję, że dobrze jest

3Silnia&6: pewnie ,ze jest dobrze.

Mila: 1) Dobrze. 2) Patrz rysunek Bogdana GC||AB

	CE		1
ΔABE ∼Δ CGE w skali k=		=		cecha kkk⇔
	AE		2

GC		1
	=		⇔|GC|=3x
AB		2

	1		p+q
GE=		|EB|=
	2		2

	GC		3x
ΔDBF ∼Δ CGF w skali k=		=		=34⇔
	DB		4x

	3		3
|GF|=		*|FB|=		q
	4		4

	4
q=		(p+q2+p)
	3

⇔q=6p ⇔EF:FB=p:(6p)=1:6 cnw

Mila: