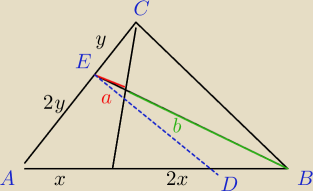
 Wykaż, że a=6b.
Dorysowuję więc do rysunku równoległą do boku BC odcinek DE przechodzący przez punkt
przeciecia.
Mam trójkaty ADE i ACB podobne. Nie wiem co zrović dalej
Wykaż, że a=6b.
Dorysowuję więc do rysunku równoległą do boku BC odcinek DE przechodzący przez punkt
przeciecia.
Mam trójkaty ADE i ACB podobne. Nie wiem co zrović dalej 
 EC| = 1:2
i |AD|
EC| = 1:2
i |AD| DB| = 1:2 wykaż, że a:b = 1:6
Punkt D jest na rysunku zaznaczony. Powinien być w spodku odcinka który ma początek w punkcie C
i opada na podstawę AB.
DB| = 1:2 wykaż, że a:b = 1:6
Punkt D jest na rysunku zaznaczony. Powinien być w spodku odcinka który ma początek w punkcie C
i opada na podstawę AB.
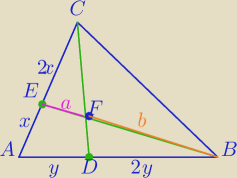 Znowu twórczość własna? Zobacz czy tak ma być?
|EF|=a
|FB|=b
Znowu twórczość własna? Zobacz czy tak ma być?
|EF|=a
|FB|=b
| a | 1 | ||
= | ⇔ | ||
| b | 6 |
 Ja tutaj przyszedłem podpatrzyć rozwiązanie
Ja tutaj przyszedłem podpatrzyć rozwiązanie 
| a | PΔCEF | ||
= | |||
| b | PΔCFB |
 S− I nie odzywa się , tam inna treść niż narysowałam.
Teraz mam inny pomysł.
S− I nie odzywa się , tam inna treść niż narysowałam.
Teraz mam inny pomysł.
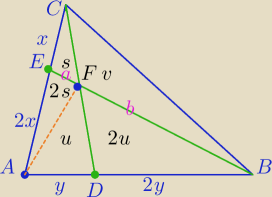 W trójkącie ABC punkty D, E leżą odpowiednio na bokach AB i AC tak, że |AD|: |DB|=1:2
oraz |AE|: |EC|=2:1. Udowodnij, że |EF|: |FB|=1:6
EF=a, FB=b
P− pole ΔABC
W trójkącie ABC punkty D, E leżą odpowiednio na bokach AB i AC tak, że |AD|: |DB|=1:2
oraz |AE|: |EC|=2:1. Udowodnij, że |EF|: |FB|=1:6
EF=a, FB=b
P− pole ΔABC
| PΔEFC | EF | ||
= | − Δmają tę samą wysokość | ||
| PΔCFB | FB |
| 1 | 2 | |||
PΔADC= | P=PΔCEB, PΔAEB= | P | ||
| 3 | 3 |
| 1 | 2 | |||
3s+u= | P i 2s+3u= | P | ||
| 3 | 3 |
| 1 | ||
s= | P | |
| 21 |
| 1 | 1 | 1 | 6 | |||||
s+v= | P⇔v= | P− | P= | P | ||||
| 3 | 3 | 21 | 21 |
| PΔEFC | a |
| |||||||||
= | = | ||||||||||
| PΔCFB | b |
|
| a | 1 | ||
= | |||
| b | 6 |
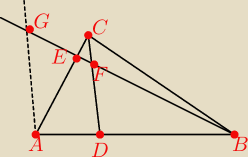 Dorysowuje odcinek GA równoległy do CD. Więc trójkąty GBA i FBD są podobne =>
Dorysowuje odcinek GA równoległy do CD. Więc trójkąty GBA i FBD są podobne =>
| |GB| | FB | ||
= | |||
| 3*|AD| | 2*|AD| |
| 3*|FB| | ||
|GB| = | ||
| 2 |
| |FB| | ||
|GF| = | ||
| 2 |
| |FB| | ||
|GE| = | − |EF| | |
| 2 |
| |EF| | |GE| | |||
Co implikuje że trójkąty CEF i GEA są podobne. Więc | = | |||
| |CE| | |AE| |
| |EF| | |GE| | ||
= | |||
| |CE| | 2|CE| |
| |FB| | ||
− |EF| = 2|EF| | ||
| 2 |
| |FB| | |
= 3|EF| /*2 | |
| 2 |