Równanie z liczbami zespolonymi Łukasz: Rozwiąż równanie z⁴ = −16. Otrzymane pierwiastki zaznacz, na płaszczyźnie zespolonej. Doszedłem do momentu: z = ⁴√−16 z = 2 ⁴√ −1 z = 2 ⁴√i² z = 2 √i

Jack: tak sie tego nie liczy, bo pominiesz rozw. 2 sposoby : 1) pierwiastkowanie zespolonych (tak jak masz potegowanie Moivrem tak tez jest dzielenie) 2) umiejetnie przeksztalcac wykorzystujac wzory skroconego mnozenia

Jack: https://www.matemaks.pl/pierwiastkowanie-liczb-zespolonych.html spojrz na wzorek do pierwiastkowania

kochanus_niepospolitus: https://matematykaszkolna.pl/forum/352642.html aż tak trudno spojrzeć czy ktoś nie dał tego samego zadania (i to dzisiaj)

Powracający: z⁴−16i²=0 (z²−4i)(z²+4i)=0

Adamm: z⁴+16=0 z⁴−16i²=0 (z²−4i)(z²+4i)=0 teraz zauważając że (i+1)²=2i oraz (i−1)²=−2i (z²−(√2i+√2)²)(z²−(√2i−√2)²)=0 (z−√2i−√2)(z−√2i+√2)(z+√2i−√2)(z+√2i+√2)=0 z=−√2i−√2 lub z=−√2i+√2 lub z=√2i−√2 lub z=√2i+√2

Mila: z⁴+16=0 z⁴−i²*16=0 (z²−4i)*(z²+4i)=0 z²=4i lub z²=−4i z=√4i lub z=√−4i 1) z=√4i |4i|=4

	π
φ=
	2

	π   +2kπ 2		π   +2kπ 2
zk=√4*(cos		+i sin		), k∊{0,1}
	2		2

	π		π
z0=2*(cos		+i sin		)
	4		4

z₀=√2+i √2 licz dalej sam?

Łukasz: @Mila czemu |4i| = 4 i skąd wziął się kąt π/2? Drugi pierwiastek z przypadku z=√4i wyszedł mi −√2+i√2, więc zgadza się z tym co napisał Adamm

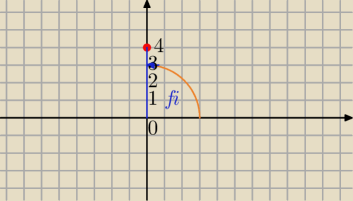Mila: z=0+4i to na płaszczyźnie punkt (0,4) |z|=√0²+4²=4 interpretacja geometryczna liczb zespolonych https://www.matemaks.pl/interpretacja-geometryczna-liczby-zespolonej.html