Jak obliczyć długość przekątnej?
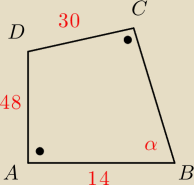
Robert: Dany jest czworokąt ABCD, w którym długości boków wynoszą: |AB|=14, |CD|=30, |AD|=48 oraz kąty
DAB i BCD są proste. Oblicz pole tego czworokąta oraz długości jego przekątnych.
Pytanie brzmi jak dokładnie obliczyć długość przekątnej AC? Z resztą sobie już poradziłem.
Bok |BC| ma długość 40. Obliczyłem sobie ile mają kąty DBC i ABD, a później z twierdzenia
cosinusów policzyłem długość przekątnej, ale wynik jest niedokładny.
25 kwi 17:33
Robert: Może dodam, że przekątna DB ma długość 50.
25 kwi 17:45
Adamm:
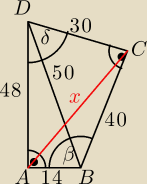
|DB|=50
|BC|=40
z tw. Cosinusów
14
2+40
2−2*14*40*cosα=|AC|
2
| 142+402−|AC| | |
| =cosα |
| 2*14*40 | |
48
2+30
2+2*48*30*cosα=|AC|
2
| |AC|2−482−302 | |
| =cosα |
| 2*48*30 | |
| |AC|2−482−302 | | 142+402−|AC|2 | |
| = |
| |
| 2*48*30 | | 2*14*40 | |
7|AC|
2−7*48
2−7*30
2=18*14
2+18*40
2−18*|AC|
2
|AC|=46,8
25 kwi 17:45
g:
pole = 48*14/2 + 30*40/2
β+δ = 180 ⇒ cos δ = −cos β
x
2 = 14
2+40
2−2*14*40*cos β = 30
2+48
2+2*30*48*cos β
wyznacz cos β, a następnie x
2.
25 kwi 18:06
25 kwi 19:13
 |DB|=50
|BC|=40
z tw. Cosinusów
142+402−2*14*40*cosα=|AC|2
|DB|=50
|BC|=40
z tw. Cosinusów
142+402−2*14*40*cosα=|AC|2
 pole = 48*14/2 + 30*40/2
β+δ = 180 ⇒ cos δ = −cos β
x2 = 142+402−2*14*40*cos β = 302+482+2*30*48*cos β
wyznacz cos β, a następnie x2.
pole = 48*14/2 + 30*40/2
β+δ = 180 ⇒ cos δ = −cos β
x2 = 142+402−2*14*40*cos β = 302+482+2*30*48*cos β
wyznacz cos β, a następnie x2.